
分析 解不等式即可得出x≥$\frac{14+3m}{3+2m}$,由不等式的一个解为x=-4即可得出$\frac{14+3m}{3+2m}$≤-4,解之即可得出m的取值范围.
解答 解:∵$\frac{x-m}{2}$≥$\frac{7-mx}{3}$,
∴x≥$\frac{14+3m}{3+2m}$.
∵关于x的不等式$\frac{x-m}{2}$≥$\frac{7-mx}{3}$的一个解为x=-4,
∴$\frac{14+3m}{3+2m}$≤-4,
解得:-$\frac{26}{11}$≤m<-$\frac{3}{2}$.
∴m的取值范围为-$\frac{26}{11}$≤m<-$\frac{3}{2}$.
点评 本题考查了不等式的解集,根据不等式的一个解为x=-4得出关于m的不等式是解题的关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.AC=3,AB=6,则AD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.AC=3,AB=6,则AD=( )| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{9}{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
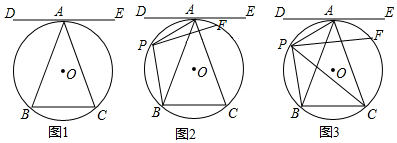
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
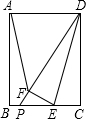 如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$.
如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
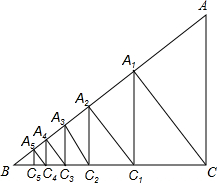 如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C2作C2A2⊥AB,垂足为A2,再过A3作A3C3⊥BC,垂足为C3,…,这样一直做下去,得到了一组线段CA1,A1C1,C2A2,…,则$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.
如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C2作C2A2⊥AB,垂足为A2,再过A3作A3C3⊥BC,垂足为C3,…,这样一直做下去,得到了一组线段CA1,A1C1,C2A2,…,则$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=50,BC=64,连结BD,AE⊥BD垂足为E,
已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=50,BC=64,连结BD,AE⊥BD垂足为E,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com