
 如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,OA=$\frac{1}{2}$OC=4,∠AOC=∠B=60°,点D是线段OC中点,连接AD.
如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,OA=$\frac{1}{2}$OC=4,∠AOC=∠B=60°,点D是线段OC中点,连接AD.分析 (1)如图2中,作AM⊥OD于M,作AN⊥BC于点N,首先证明四边形AMCN是矩形,△AOD是等边三角形,求出AM,CM,在Rt△ABN中,求出BN即可解决问题.
(2)①如图3中延长BA交x轴于P,直线l交x轴于F,交AB于E.分别解直角三角形△BCP,△EFP即可;
②当6≤t≤12时,在Rt△PEF中,EF=$\frac{1}{2}$PF,延长即可解决问题;
解答 解:(1)如图2中,作AM⊥OD于M,作AN⊥BC于点N,
∵OA=4,OC=8,OD=DC,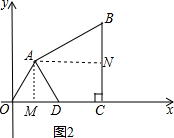
∴OA=OD=4,
∵∠AOD=60°,
∴△AOD是等边三角形,
∵BC⊥OC,
∴∠AMC=∠ANC=∠NCM=90°,
∴四边形AMCN是矩形,
∴AM=CN=2$\sqrt{3}$,CM=AN=6,
在Rt△ABN中,BN=AN•tan30°=2 $\sqrt{3}$,AB=2BN=4$\sqrt{3}$,
∴BC=BN+CN=4 $\sqrt{3}$,
∴点B的坐标为(8,4 $\sqrt{3}$).
(2)①如图3中,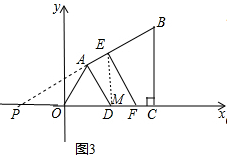 延长BA交x轴于P,直线l交x轴于F,交AB于E.
延长BA交x轴于P,直线l交x轴于F,交AB于E.
∵∠BPC=30°,∠PDA=60°,
∴∠PAD=90°,
∵EF∥AD,
∴∠PEF=∠PAD=90°,
在Rt△PBC中,PC=BC•tan60°=12,
∴OP=PC-OC=4,
∵t=6,
∴OF=6,PF=10,
在Rt△PEC中,EF=$\frac{1}{2}$PF=5.
②当6≤t≤12时,在Rt△PEF中,EF=$\frac{1}{2}$PF=$\frac{1}{2}$(t+4)=$\frac{1}{2}$t+2.
点评 本题考查四边形综合题、等边三角形的判定和性质、解直角三角形、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
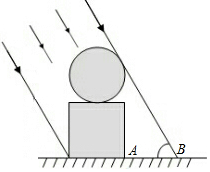 如图,广场上一个立体雕塑由两部分组成,底座是一个正方体,正上方是一个球体,且正方体的高度和球的高度相等.当阳光与地面的夹角成60°时,整个雕塑在地面上的影子AB长2米,求这个雕塑的高度.(结果精确到百分位,参考数据:$\sqrt{3}$≈1.73)
如图,广场上一个立体雕塑由两部分组成,底座是一个正方体,正上方是一个球体,且正方体的高度和球的高度相等.当阳光与地面的夹角成60°时,整个雕塑在地面上的影子AB长2米,求这个雕塑的高度.(结果精确到百分位,参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 份数/份 | 1 | 2 | 3 | 4 | … |
| 价钱/元 | 0.4 | 0.8 | 1.2 | 1.6 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com