
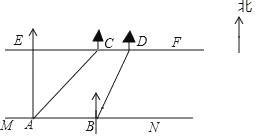
【题目】在社会实践课上,小聪所在小组要测量一条小河的宽度,如图,河岸EF∥MN,小聪在河岸MN上的点A处测得河对岸小树C位于东北方向,然后向东沿河岸走了30米,到达B处测得河对岸小树D位于北偏东30°的方向,又有同学测得CD=10米
(1)∠EAC= 度,∠DBN= 度;
(2)求小河的宽度AE.(结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
【答案】(1)45,60;(2)河的宽度AE约为47.3米.
【解析】
(1)由题意即可得出结果;
(2)作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,根据tan30°=![]() 列出方程,即可解决问题.
列出方程,即可解决问题.
(1)由题意得:∠BAC=∠EAC=45°,∠DBN=90°﹣30°=60°;
故答案为:45,60;
(2)如图,作BH⊥EF于H,CK⊥MN于K,垂足分别为H、K,
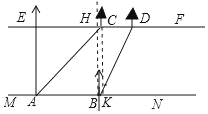
则四边形BHCK是矩形,AE=HB,
设CK=HB=x,
∵∠CKA=90°,∠CAK=45°,
∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,
∴HD=x﹣30+10=x﹣20,
在Rt△BHD中,∵∠BHD=90°,∠HBD=30°,
∴tan30°=![]() ,
,
∴![]() ,
,
解得x=30+10![]() ≈47.3,
≈47.3,
∴AE=HB≈47.3米;
答:河的宽度AE约为47.3米.


科目:初中数学 来源: 题型:
【题目】“食品安全真重要,病从口入危害大.良好习惯要养成,食品挑选切注意.”是食品卫生安全歌谣中的一段歌词,某中学针对一些学生不吃正餐,爱吃街边小吃及一些三无小食品,严重危害身体健康的情况,为提高学生们的食品安全意识组织了食品安全教育活动.学校就“是否会根据食品的三无情况来挑选日常食品”的问题在活动前随机抽取一部分学生进行调查,大致有以下五种观点:A:不吃“三无”食品;B:“三无”食品不太安全,可以少吃,但不能多吃;C:看着干净、卫生的食品就可以放心食用;D:高档的,贵的食品都可放心食用;E:不用关注食品的“三无”情况活动后再次调查这部分学生持这几种观点的情况,并将统计结果绘制成如下不完整的统计图(每位同学仅持一种观点).
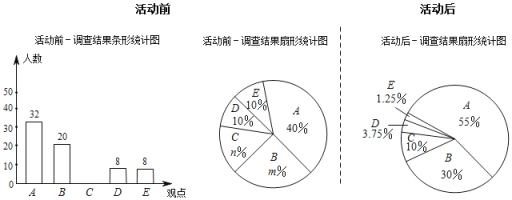
根据以上统计图,解答下列问题:
(1)活动前后,每次接受调查的学生总人数都为_____人,m=_____,n=_____;
(2)请补全活动前的调查结果条形统计图.
(3)若全校共有3200人,请你估计通过这次活动后,还有多少人持E种观点?
(4)根据活动前后的相关数据,说明活动的效果,并提出合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(﹣5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=![]() 上,若线段AC扫过的面积为48,则点C1的坐标为( )
上,若线段AC扫过的面积为48,则点C1的坐标为( )
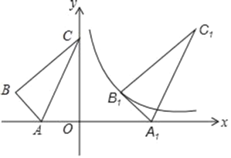
A.(3,2)B.(5,6)C.(8,6)D.(6,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD中,直线l⊥边AB,并从点A出发向右平移,设直线l在菱形ABCD内部截得的线段EF的长为y,平移距离x=AF,y与x之间的函数关系的图象如图2所示,则菱形ABCD的面积为( )
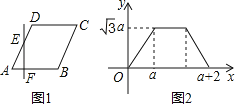
A.3B.![]() C.2
C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学图书室计划购买了甲、乙两种故事书.若购买7本甲种故事书和4本乙种故事书需510元;购买3本甲种故事书和5本乙种故事书需350元.
(1)求甲种故事书和乙种故事书的单价;
(2)学校准备购买甲、乙两种故事书共200本,且甲种故事书的数量不少于乙种故事书的数量的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
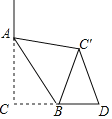
【题目】如图,CD=4,∠C=90°,点B在线段CD上,![]() ,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为_____.
,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
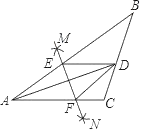
【题目】如图,在△ABC中,AD平分∠BAC,按如下步作图:①分别以点A,D为圆心,以大于![]() AD的长为半径在AD两侧作弧,两弧交于两点M,N;②作直线MN分别交AB,AC于点E,F;③连接DE,DF,若BD=6,AE=4,CD=3,则CF的长是( )
AD的长为半径在AD两侧作弧,两弧交于两点M,N;②作直线MN分别交AB,AC于点E,F;③连接DE,DF,若BD=6,AE=4,CD=3,则CF的长是( )
A.1B.1.5C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
查看答案和解析>>
科目:初中数学 来源: 题型:
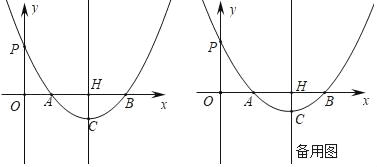
【题目】如图,在平面直角坐标系中,二次函数y=a(x﹣1)(x﹣5)(a>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于P点,过其顶点C作直线CH⊥x轴于点H.
(1)若∠APB=30°,请直接写出满足条件的点P的坐标;
(2)当∠APB最大时,请求出a的值;
(3)点P、O、C、B能否在同一个圆上?若能,请求出a的值,若不能,请说明理由.
(4)若a=![]() ,在对称轴HC上是否存在一点Q,使∠AQP=∠ABP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
,在对称轴HC上是否存在一点Q,使∠AQP=∠ABP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com