
【题目】某玩具厂计划一周生产某种玩具700件,平均每天生产100件,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | -2 | -4 | +13 | -6 | +6 | -3 |
(1)根据记录的数据可知该厂星期四生产玩具 件;
(2)产量最多的一天比产量最少的一天多生产玩具 件;
(3)根据记录的数据可知该厂本周实际生产玩具 件;
(4)该厂实行每周计件工资制,每生产一件玩具可得20元,若超额完成任务,则超过部分每件另奖5元;少生产一件扣4元,那么该厂工人这一周的工资总额是多少元?
【答案】(1)113;(2)19;(3)709 ;(4)14225元
【解析】
(1)根据“超产记为正、减产记为负”,从而用100加上13进一步计算即可;
(2)根据表格信息得知,周四产量最多,而周五最少,所以据此进一步计算即可;
(3)根据表格之中每天的实际产量情况进一步计算即可;
(4)根据(3)得出实际产量,然后按照奖罚制度进一步计算即可;
(1)∵超产记为正、减产记为负,
∴100+13=113(件),
故答案为:113;
(2)根据表格信息得知,周四产量最多,而周五最少,
∴![]() (件),
(件),
故答案为:19;
(3)由题意得:524+136+63=9(件),
∴100×7+9=709(件),
故答案为:709;
(4)由(3)得实际产量为709件,超额完成部分为9件,
∴![]() (元)
(元)
答:该厂工人这一周的工资总额是14225元


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】某中学学生步行到郊外旅行,七年级![]() 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米![]() 小时,七
小时,七![]() 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米![]() 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米![]() 小时.
小时.
![]() 后队追上前队需要多长时间?
后队追上前队需要多长时间?
![]() 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少?
![]() 七年级
七年级![]() 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是定长线段
是定长线段![]() 上一定点,点
上一定点,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,点
上,点![]() 、点
、点![]() 分别从点
分别从点![]() 、点
、点![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动,运动方向如箭头所示.
向左运动,运动方向如箭头所示.
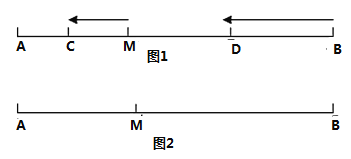
(1)若![]() ,当点C、D运动了2s,求
,当点C、D运动了2s,求![]() 的值;
的值;
(2)若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,直接填空:
,直接填空:![]() ______
______![]() ;
;
(3)在(2)的条件下,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出定义:我们用(a,b)来表示一对有理数a,b,若a,b满足a﹣b=ab+1,就称(a,b)是“泰兴数”如2﹣![]() +1,则(2,
+1,则(2,![]() )是“泰兴数”.
)是“泰兴数”.
(1)数对(﹣2,1),(5,![]() )中是“泰兴数”的是 .
)中是“泰兴数”的是 .
(2)若(m,n)是“泰兴数”,求6m﹣2(2m+mn)﹣2n的值;
(3)若(a,b)是“泰兴数”,则(﹣a,﹣b) “泰兴数”(填“是”或“不是”).
查看答案和解析>>
科目:初中数学 来源: 题型:
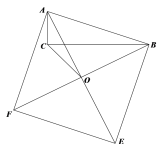
【题目】如图,以Rt![]() 的斜边AB为一边在
的斜边AB为一边在![]() 同侧作正方形ABEF.点O为AE与BF的交点,连接CO,若CA = 2,
同侧作正方形ABEF.点O为AE与BF的交点,连接CO,若CA = 2,![]() ,那么四边形ABOC的面积为_______.
,那么四边形ABOC的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向
向![]() 点运动,速度为
点运动,速度为![]() ;动点
;动点![]() 从
从![]() 点出发,沿线段
点出发,沿线段![]() 向点
向点![]() 运动,速度为
运动,速度为![]() .
.![]() 同时出发,设运动的时间是
同时出发,设运动的时间是![]()
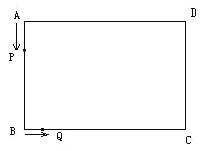
(1)请用含![]() 的代数式表示下列线段的长度,当点
的代数式表示下列线段的长度,当点![]() 在
在![]() 上运动时,
上运动时,![]() ,
,![]() ,当
,当![]() 运动到
运动到![]() 上时,
上时,![]() ,
,![]() .
.
(2)当点![]() 在
在![]() 上运动时,
上运动时,![]() 为何值,能使
为何值,能使![]() ?
?
(3)点![]() 能否追上点
能否追上点![]() ?如果能,求出
?如果能,求出![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
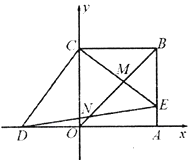
【题目】如图,在平面直角坐标系中,正方形![]() 两顶点为
两顶点为![]() ,
,![]() ,点D的坐标为
,点D的坐标为![]() ,在
,在![]() 上取点E,使得
上取点E,使得![]() ,连接
,连接![]() ,分别交
,分别交![]() ,
,![]() 于M,N两点.
于M,N两点.
(1)求证:![]() ;
;
(2)求点E的坐标和线段![]() 所在直线的解析式;
所在直线的解析式;
(3)在M,N两点中任选一点求出它的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com