
【题目】在正方形ABCD中,E,F分别为BC,CD的中点,AE与BF相交于点G.
(1)如图1,求证:AE⊥BF;
(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值
【答案】
(1)证明:
∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在△ABE和△BCF中,

∴Rt△ABE≌Rt△BCF(SAS),
∴∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF;
(2)解:
∵将△BCF沿BF折叠,得到△BPF,
∴FP=FC,∠PFB=∠BFC,∠FPB=90°,
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,
设QF=x,PB=BC=AB=4,CF=PF=2,
∴QB=x,PQ=x﹣2,
在Rt△BPQ中,
∴x2=(x﹣2)2+42,
解得:x=5,
即QF=5.
【解析】(1)首先依据正方形的性质可得到∠ABE=∠BCF,BC=CD,然后再依据中点的定义得到CF=BE,接下来,由SAS可证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可证明AE⊥BF;
(2)由折叠的性质可得到FP=FC,∠PFB=∠BFC,∠FPB=90,然后再依据等角对等边的性质可得到QF=QB,设QF=x,在Rt△BPQ中,利用勾股定理可建立关于x的方程解方程求出x的值即可.
【考点精析】本题主要考查了正方形的性质和翻折变换(折叠问题)的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某市规定:出租车起步价允许行驶的最远路程为3km,超过3km的部分每千米另收费,甲说:“我乘这种出租车走了9km,付了14元.”乙说:“我乘这种出租车走了13千米,付了20元”.请你算出这种出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 . 
(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(x1 , y1),(x2 , y2),(x3 , y3)都是反比例函数y=﹣ ![]() 图象上的点,并且y1<0<y2<y3 , 则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3 , 则下列各式中正确的是( )
A.x1<x2<x3
B.x1<x3<x2
C.x2<x1<x3
D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
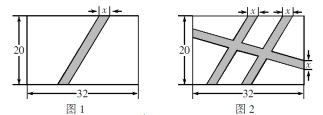
【题目】学校课外生物小组的试验园地是长32m、宽20m的矩形,为便于管理,现要在试验园地开辟水平宽度均为xm的小道(图中阴影部分).
(1)如图1,在试验园地开辟一条水平宽度相等的小道,则剩余部分面积为 m2(用含x的代数式表示);
(2)如图2,在试验园地开辟水平宽度相等的三条小道,其中有两条道路相互平行. 若使剩余部分面积为570m2,试求小道的水平宽度x.
查看答案和解析>>
科目:初中数学 来源: 题型:
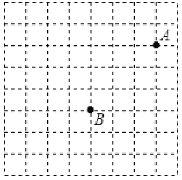
【题目】在正方形网格中建立平面直角坐标系![]() ,使得
,使得![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴于点C,
轴于点C,
(1)按照要求画出平面直角坐标系![]() ,线段
,线段![]() ,写出点
,写出点![]() 的坐标__________;
的坐标__________;
(2)直接写出以![]() ,
,![]() ,
,![]() 为顶点的三角形的面积___________;
为顶点的三角形的面积___________;
(3)若线段![]() 是由线段
是由线段![]() 平移得到的,点
平移得到的,点![]() 的对应点是
的对应点是![]() ,写出一种由线段
,写出一种由线段![]() 得到线段
得到线段![]() 的过程________.
的过程________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月全国两会胜利召开,某数学兴趣小组就两会期间出现频率最高的热词:A脱贫攻坚.B.绿色发展.C.自主创新.D.简政放权等热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com