
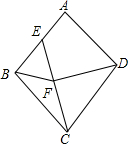
 已知,如图,在菱形ABCD中,点E为AB边的中点,连接CE,点F为CE上的一点且2∠BFE+∠A=180°,连接DF,则∠CFD=
已知,如图,在菱形ABCD中,点E为AB边的中点,连接CE,点F为CE上的一点且2∠BFE+∠A=180°,连接DF,则∠CFD=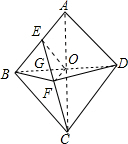 解:如图,连接AC、BD,AC与BD交于点O,连接EO、FO.
解:如图,连接AC、BD,AC与BD交于点O,连接EO、FO.| GO |
| GC |
| GF |
| GD |
| GO |
| GF |
| GC |
| GD |


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
 在一幅长为80cm、宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为x cm,那么x满足的方程是( )
在一幅长为80cm、宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为x cm,那么x满足的方程是( )| A、x2+65x-350=0 |
| B、x2+130x-1400=0 |
| C、x2-65x-350=0 |
| D、x2-130x-1400=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2b |
| a2-b2 |
| 1 |
| a+b |
| x2 |
| x2-1 |
| 1 |
| x-1 |
| x2-9 |
| x2+8x+16 |
| x-3 |
| x+4 |
| x |
| x+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
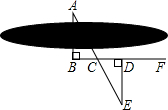 如图,要测量河岸相对两点A,B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在同一直线上,可以证明△EDC≌△ABC得ED=AB,因此测得DE的长度就是AB的长,判断△EDC≌△ABC的理由是( )
如图,要测量河岸相对两点A,B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在同一直线上,可以证明△EDC≌△ABC得ED=AB,因此测得DE的长度就是AB的长,判断△EDC≌△ABC的理由是( )| A、边边边 | B、边角边 |
| C、角边角 | D、边边角 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2.42亿元 |
| B、2.4亿元 |
| C、2.2亿元 |
| D、4.4亿元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com