练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    一次函数的图象经过A（3，5）和B（-4，-9）.
    （1）求这个函数的解析式；
    （2）若点（a，2）在该函数的图象上，试求a的值。
    （1）；（2）

    试题分析：（1）设函数关系式为，再由图象经过A（3，5）和B（-4，-9）即可根据待定系数法求得函数关系式；
    （2）把代入（1）中的函数关系式即可求得结果.
    （1）设函数关系式为，
    ∵图象经过A（3，5）和B（-4，-9）
    ∴，解得
    ∴这个函数的解析式为；
    （2）当时，，解得
    则
    点评：本题属于基础应用题，只需学生熟练掌握待定系数法求函数关系式，即可完成．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：计算题

    如图，直线是一次函数的图象，直线是一次函数
    的图象。

    （1）求、、三点坐标。（2）求的面积。

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    在一条笔直的河道上依次有A、B、C三个港口，甲、乙两船同时分别从A、B 港口出发，沿直线匀速驶向C港，最终到达C港．设甲、乙两船行驶x(h)后，与B港的距离分别为y1、y2(km)，y1、y2与x的函数关系如图所示(点P、Q为图象的交点)．

    （1）填空：A、C两港口间的距离为      km，a＝    ；
    （2）求y1与x的函数关系式，并写出自变量x的取值范围；
    （3）求图中点P的坐标，并解释该点坐标所表示的实际意义。

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    小聪和小明沿同一条路同时从学校出发到新华书店买书，学校与书店的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达书店，图中折线O－A－B－C和线段OD分别表示两人离学校的路程s（千米）与所经过的时间t（分钟）之间的函数关系，请根据图象回答下列问题：

    （1）小聪在新华书店买书的时间为________分钟，小聪返回学校的速度为_______千米/分钟；
    （2）请你求出小明离开学校的路程（千米）与所经过的时间（分钟）之间的函数关系；
    （3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，已知点A（0，6），B（4，－2），C（7，），过点B作x轴的垂线，交直线AC于点E，点F与点E关于点B对称．

    （1）求证：∠CFE=∠AFE；
    （2）在y轴上是否存在这样的点P，使△AFP与△FBC相似，若有，请求出所有符合条件的点P的坐标；若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    方程的解是直线（   ）.
    A．与轴交点的横坐标B．与轴交点的纵坐标
    C．与轴交点的横坐标D．与轴交点的纵坐标

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知一次函数，请你画出它的图象，并根据图象求：
    （1）方程的解；
    （2）不等式的解集；
    （3）不等式的解集.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    某市医药公司的甲、乙两仓库分别存有某种药品80箱和70箱，现需要将库存的药品调往A地100箱和B地50箱．
    （1）设从甲仓库运送到A地的药品为箱，请填写下表：

    		甲仓库
    		乙仓库
    		总计
    地
    		箱
    		①      箱
    		100箱
    地
    		②      箱
    		③      箱
    		50箱
    总计
    		80箱
    		70箱
    		150箱
    （2）已知从甲、乙两仓库运送药品到两地的费用（元／箱）如右表所示．求总费用（元）与（箱）之间的函数关系式，并写出的取值范围；
    （3）求出最低总费用，并说明总费用最低时的调配方案．
    地名
    		费用（元/箱）
    甲库
    		乙库
    A地
    		14
    		20
    B地
    		10
    		8
     

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    在平面直角坐标系中，对于任意两点与的“非常距离”，给出如下定义：
    若，则点与点的非常距离为；
    若，则点与点的非常距离为；
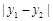    例如：点（1，2），点（3，5），因为，所以点与点的“非常距离”为，也就是图1中线段与线段长度的较大值（点Q为垂直于y轴的直线与垂直于x轴的直线的交点）．
    （1）已知点A（，0），B为y轴上的一个动点，
    ①若点A与点B的“非常距离”为2，写出满足条件的点B的坐标；
    ②直接写出点A与点B的“非常距离”的最小值．
    （2）已知C是直线上的一个动点，
    ①如图2，点D的坐标是（0，1），求点C与点D的“非常距离”的最小值及相应的点C的坐标；
    ②如图3，E是以原点O为圆心，1为半径的圆上的一个动点，求点C与点E的“非常距离”的最小值及相应点E和点C的坐标．

    查看答案和解析>>

    同步练习册答案