
分析 由方程有实根利用根的判别式△≥0,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;由方程的两根同为正利用根的判别式△≥0以及两根之积为正,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围;由方程的两根异号利用根的判别式△≥0以及两根之积为负,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围.
解答 解:∵方程x2-4x-m=0有实根,
∴△=(-4)2+4m≥0,
解得:m≥-4;
∵方程x2-4x-m=0的两根同为正,
∴$\left\{\begin{array}{l}{△=16+4m≥0}\\{-m>0}\end{array}\right.$,
解得:-4≤m<0;
∵方程x2-4x-m=0的两根异号,
∴$\left\{\begin{array}{l}{△=16+4m>0}\\{-m<0}\end{array}\right.$,
解得:m>0.
故答案为:≥-4;-4≤m<0;>0.
点评 本题考查了根的判别式以及根与系数的关系,牢记“当△≥0时,方程有实数根”是解题的关键.


科目:初中数学 来源: 题型:解答题
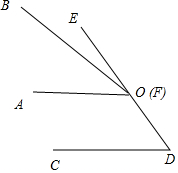 两个角∠BOA和∠EDC,∠AOB保持不动,∠EDC的一边CD∥AO,另一边DE与直线OB相交于点F.
两个角∠BOA和∠EDC,∠AOB保持不动,∠EDC的一边CD∥AO,另一边DE与直线OB相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 厂家 | 超过标准质量的部分 | |||||
| 甲 | -3 | 0 | 0 | 1 | 2 | 0 |
| 乙 | -2 | 1 | -1 | 0 | 1 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 级数 | 全月应纳税所得额 | 税率% |
| 1 | 不超过500元的部分 | 5 |
| 2 | 超过500元至2000元的部分 | 10 |
| 3 | 超过2000元至5000元的部分 | 15 |
| 4 | 超过5000元至20000元的部分 | 20 |
| … | … |
| 公民 | 工资薪金(元) | 应纳税金(元) |
| 甲 | 2000 | 0 |
| 乙 | 2500 | 25 |
| 丙 | 3900 | 165 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com