
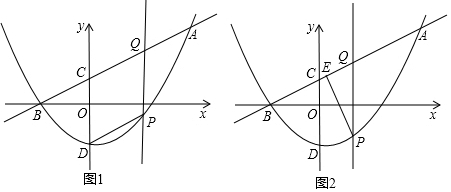
分析 (1)根据抛物线y=$\frac{1}{6}$x2+bx+c经过点A(8,6)交x负半轴于点B(-4,0),运用待定系数法求得抛物线的解析式,和直线的解析式即可;
(2)根据四边形CDPQ为平行四边形,利用PQ=CD,列出方程$-\frac{1}{6}{m^2}+\frac{2}{3}m+\frac{16}{3}$=$\frac{16}{3}$,解得:m1=4,m2=0(舍去),即可得到m的值为4;
(3)根据抛物线的解析式:$y=\frac{1}{6}{x^2}-\frac{1}{6}x-\frac{10}{3}$,设P(a,b)(-4<a<8),得到b=$\frac{1}{6}{a}^{2}-\frac{1}{6}a-\frac{10}{3}$①,再根据直线AB的解析式:$y=\frac{1}{2}x+2$,得到Q(a,$\frac{1}{2}$a+2),根据PE⊥AB,得到直线PE的解析式为y=-2x+2a+b,再解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=-2x+2a+b}\end{array}\right.$,可得E的坐标,最后根据PE恰好被x轴平分,得出$\frac{2a+b+8}{5}$+b=0②,最后联立①②解方程组可得$\left\{\begin{array}{l}{a=3}\\{b=-\frac{7}{3}}\end{array}\right.$,求得Q(3,$\frac{7}{2}$),E($\frac{2}{3}$,$\frac{7}{3}$),进而得到AQ:QE:EB的比值.
解答  解:(1)∵抛物线y=$\frac{1}{6}$x2+bx+c经过点A(8,6)交x负半轴于点B(-4,0),
解:(1)∵抛物线y=$\frac{1}{6}$x2+bx+c经过点A(8,6)交x负半轴于点B(-4,0),
∴$\left\{\begin{array}{l}{6=\frac{1}{6}×64+8b+c}\\{0=\frac{1}{6}×16-4b+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{1}{6}}\\{c=-\frac{10}{3}}\end{array}\right.$,
∴抛物线的解析式:$y=\frac{1}{6}{x^2}-\frac{1}{6}x-\frac{10}{3}$,
设直线AB的解析式为y=kx+n,则
$\left\{\begin{array}{l}{6=8k+n}\\{0=-4k+n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{n=2}\end{array}\right.$,
∴直线AB的解析式:$y=\frac{1}{2}x+2$;
(2)①∵PQ⊥x轴,点P的横坐标为m,
∴P(m,$\frac{1}{6}$m2-$\frac{1}{6}$m-$\frac{10}{3}$),Q(m,$\frac{1}{2}m+2$),
∴PQ=$\frac{1}{2}m+2$-($\frac{1}{6}{m^2}-\frac{1}{6}m-\frac{10}{3}$)=$-\frac{1}{6}{m^2}+\frac{2}{3}m+\frac{16}{3}$;
②在抛物线$y=\frac{1}{6}{x^2}-\frac{1}{6}x-\frac{10}{3}$中,当x=0时,y=-$\frac{10}{3}$,
即D(0,-$\frac{10}{3}$),
在直线AB的解析式$y=\frac{1}{2}x+2$中,当x=0时,y=2,
即C(0,2),
∴CD=2-($-\frac{10}{3}$)=$\frac{16}{3}$
∵四边形CDPQ为平行四边形,
∴PQ=CD,
∴$-\frac{1}{6}{m^2}+\frac{2}{3}m+\frac{16}{3}$=$\frac{16}{3}$,
解得:m1=4,m2=0(舍去),
∴m的值为4;
(3)∵抛物线的解析式:$y=\frac{1}{6}{x^2}-\frac{1}{6}x-\frac{10}{3}$,
∴设P(a,b)(-4<a<8),则b=$\frac{1}{6}{a}^{2}-\frac{1}{6}a-\frac{10}{3}$,①
∵直线AB的解析式:$y=\frac{1}{2}x+2$,
∴Q(a,$\frac{1}{2}$a+2),
∵PE⊥AB,
∴直线PE的解析式为y=-2x+2a+b,
解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=-2x+2a+b}\end{array}\right.$,可得E($\frac{4a+2b-4}{5}$,$\frac{2a+b+8}{5}$),
∵PE恰好被x轴平分,
∴$\frac{2a+b+8}{5}$+b=0,②
联立①②解方程组可得$\left\{\begin{array}{l}{a=3}\\{b=-\frac{7}{3}}\end{array}\right.$,$\left\{\begin{array}{l}{a=-4}\\{b=0}\end{array}\right.$(舍去),
∴Q(3,$\frac{7}{2}$),E($\frac{2}{3}$,$\frac{7}{3}$),
∴AQ:QE:EB=(8-3):(3-$\frac{2}{3}$):($\frac{2}{3}$+4)=15:7:14.
故答案为:15:7:14.
点评 本题主要考查了二次函数的综合应用,解决问题的关键是掌握待定系数法求函数解析式的方法,以及平行四边形的性质,解题时注意:平行四边形的对边相等,这是列方程的主要依据.解题时注意方程思想的灵活运用.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:选择题
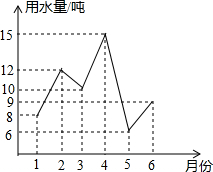 为了了解家里的用水情况,以便能更好的节约用水,小方把自己家1至6月份的用水量绘制成如图的折线图,那么小方家这6个月的月用水量最大是( )
为了了解家里的用水情况,以便能更好的节约用水,小方把自己家1至6月份的用水量绘制成如图的折线图,那么小方家这6个月的月用水量最大是( )| A. | 1月 | B. | 4月 | C. | 5月 | D. | 6月 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
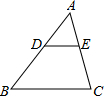 如图,在△ABC中,点D,E分别在边A B,AC上,DE∥BC,已知EC=6,$\frac{AD}{DB}=\frac{2}{3}$,则AC的长是10.
如图,在△ABC中,点D,E分别在边A B,AC上,DE∥BC,已知EC=6,$\frac{AD}{DB}=\frac{2}{3}$,则AC的长是10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com