
【题目】已知四边形![]() 是菱形,
是菱形,![]() 的两边分别与射线
的两边分别与射线![]() 相交于点
相交于点![]() ,且
,且![]()
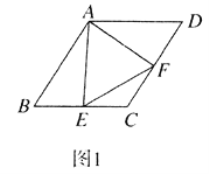
![]() 如图1,当点
如图1,当点![]() 是线段
是线段![]() 的中点时,求证:
的中点时,求证:![]() ;
;
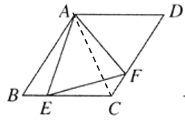
![]() 如图2,当点
如图2,当点![]() 是线段
是线段![]() 上任意一点时(点
上任意一点时(点![]() 不与
不与![]() 重合),求证:
重合),求证:![]() ;
;

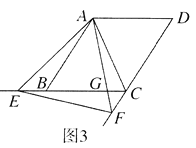
![]() 如图3,当点
如图3,当点![]() 在线段
在线段![]() 的延长线上时,设
的延长线上时,设![]() 交
交![]() 于点
于点![]() 求证:
求证:![]() .
.
【答案】(1)详见解析;(2)详见解析;(2)详见解析
【解析】
(1)通过菱形可知AB=AD,∠B=∠D,然后通过![]() 是线段
是线段![]() 的中点,可知BE=DF,即可得到
的中点,可知BE=DF,即可得到![]() ,从而可得到答案;
,从而可得到答案;
(2)连![]() ,通过条件去证
,通过条件去证![]() 即可得到
即可得到![]() ;
;
(3)通过两组对应角相等得到![]() ,然后得到
,然后得到![]() ,再由
,再由![]() 可得到AE=AF,从而得到答案.
可得到AE=AF,从而得到答案.
![]() ∵四边形
∵四边形![]() 是菱形,
是菱形,
∴AB=AD=BC=CD,∠B=∠D,
∵![]() 是线段
是线段![]() 的中点,
的中点,
∴BE=DF,
在![]() 和
和![]() 中
中

∴![]() ,
,
![]()
又![]()
![]() 为等边三角形
为等边三角形
![]()
![]() 连
连![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴AB=AD=BC=CD,∠B=∠D,
∵![]() ,
,
∴△ABC是等边三角形,同理△ADC是等边三角形,
∴∠BAC=∠ACD=60°,AB=AC,
∴∠BAE+∠EAC=60°,∠FAC+∠EAC=60°,
∴∠FAC=∠BAE,
在![]() 和
和![]() 中
中

∴![]()
∴![]()
![]() ∵四边形
∵四边形![]() 是菱形,
是菱形,
∴AB∥CD,
∴![]() ,
,
又∵![]()
∴![]()
![]()
同(2)中方法可得![]() ,
,
![]()
![]()
即![]()


科目:初中数学 来源: 题型:
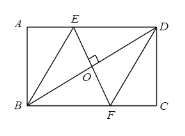
【题目】如图,在矩形ABCD中,AB=3,做BD的垂直平分线E,F,分别与AD、BC交于点E、F,连接BE,DF,若EF=AE+FC,则边BC的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
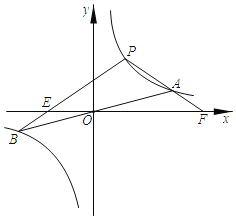
【题目】如图,双曲线y1=![]() 与直线y2=
与直线y2=![]() 的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=
的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=![]() 上的任意一点,且0<a<4.
上的任意一点,且0<a<4.
(1)分别求出y1、y2的函数表达式;
(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;
(3)当点P在双曲线y1=![]() 上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
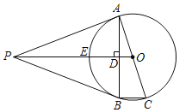
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=![]() ,BC=1,求PO的长.
,BC=1,求PO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解全国中学生视力的情况,应采用普查的方式
B.某种彩票中奖的概率是![]() ,买1000张这种彩票一定会中奖
,买1000张这种彩票一定会中奖
C.从2000名学生中随机抽取200名学生进行调查,样本容量为200名学生
D.从只装有白球和绿球的袋中任意摸出一个球,摸出黑球是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
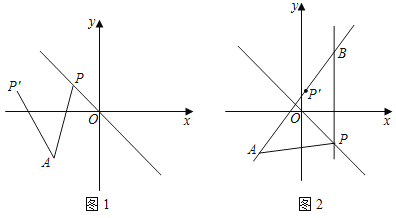
【题目】如图1,点P(m,n)在一次函数y=﹣x的图象上,将点P绕点A(﹣![]() ,﹣
,﹣![]() )逆时针旋转45°,旋转后的对应点为P′.
)逆时针旋转45°,旋转后的对应点为P′.
(1)当m=0时,求点P′的坐标;
(2)试说明:不论m为何值,点P′的纵坐标始终不变;
(3)如图2,过点P作x轴的垂线交直线AP′于点B,若直线PB与二次函数y=﹣x2﹣x+2的图象交于点Q,当m>0时,试判断点B是否一定在点Q的上方,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
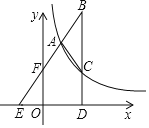
【题目】如图,在△ABC中,AB=AC,BC⊥x轴,垂足为D,边AB所在直线分别交x轴、y轴于点E、F,且AF=EF,反比例函数y=![]() 的图象经过A、C两点,已知点A(2,n).
的图象经过A、C两点,已知点A(2,n).
(1)求AB所在直线对应的函数表达式;(2)求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
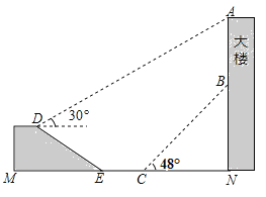
【题目】如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为48°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=![]() ,且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上.
,且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上.
(1)求BN的长度;
(2)求条幅AB的长度(结果保留根号).
(参考数据:sin48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com