

分析 (1)根据AB+AC>BC和BD=AB,得到答案;
(2)根据(1)的结论和平行四边形的对边相等证明即可;
(3)根据平行四边形的对边相等和圆的性质即可得到答案.
解答 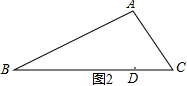 解:(1)∵AB+AC>BC,
解:(1)∵AB+AC>BC,
∴AB+AC>BD+DC,又BD=AB,
∴AC>DC.
故答案为:>;
(2)EF>EG,证明如下:
由(1)得,AC>DC,
∵四边形DCEF是平行四边形,
∴EF=CD,
∵四边形ACEG是平行四边形,
∴GE=AC,
∴EF>EG;
(3)∵四边形PABC是平行四边形,
∴BC=AP,
∴BC的最小值即AP的最小值,
∵当P为OA与⊙O的交点时AP最小,
∴AP的最小值为9-5=4,
即BC的最小值为4,
点C的位置如图4所示.
点评 本题考查的是圆的知识、平行四边形的性质和三角形三边关系,掌握三角形两边之和大于第三边、平行四边形的对边相等是解题的关键.


科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:解答题
分别以□ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.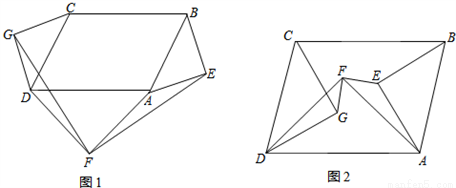
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知矩形ABCD中,AB=8,BC=12,点E、F分别为线段BC、DE的中点,连接BF、AE交于点G.
如图,已知矩形ABCD中,AB=8,BC=12,点E、F分别为线段BC、DE的中点,连接BF、AE交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+3y=5xy | B. | a2+a3=a5 | ||
| C. | (-3x2y)3=-9x6y3 | D. | 4x3y2$•(-\frac{1}{2}x{y}^{2})$=-2x4y4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com