
ЁОЬтФПЁПЮЊСЫМгЧПЙЋУёЕФНкЫЎвтЪЖЃЌКЯРэРћгУЫЎзЪдДЃЌИїЕиВЩгУМлИёЕїПиЕШЪжЖЮв§ЕМЪаУёНкдМгУЫЎЁЃФГЪаЙцЖЈШчЯТгУЫЎЪеЗбБъзМЃКУПдТУПЛЇЕФгУЫЎВЛГЌЙ§6![]() ЪБЃЌЫЎЗбАДе§ГЃЪеЗбЃЛГЌЙ§6
ЪБЃЌЫЎЗбАДе§ГЃЪеЗбЃЛГЌЙ§6![]() ЪБЃЌГЌЙ§ЕФВПЗжЪеНЯИпЫЎЗбЁЃИУЪаФГЛЇОгУёНёФъ2дТЗнЕФгУЫЎСПЮЊ9
ЪБЃЌГЌЙ§ЕФВПЗжЪеНЯИпЫЎЗбЁЃИУЪаФГЛЇОгУёНёФъ2дТЗнЕФгУЫЎСПЮЊ9![]() ЃЌНЩФЩЫЎЗбЮЊ27дЊЃЛ3дТЗнЕФгУЫЎСПЮЊ11
ЃЌНЩФЩЫЎЗбЮЊ27дЊЃЛ3дТЗнЕФгУЫЎСПЮЊ11![]() ЃЌНЩФЩЫЎЗбЮЊ37дЊЁЃ
ЃЌНЩФЩЫЎЗбЮЊ37дЊЁЃ
(1)ЧѓдкЯоЖЈСПвдФкУПЖжЖрЩйдЊЃПГЌГіВПЗжЕФЫЎЗбУПЖжЖрЩйдЊЃП
(2)ШєИУЪаФГОгУёНёФъ4дТЗнЕФгУЫЎСПЮЊ13![]() . дђгІНЩФЩЫЎЗбЖрЩйдЊЃП
. дђгІНЩФЩЫЎЗбЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉдкЯоЖЈСПвдФкУПЖж2дЊЃЌГЌГіВПЗжЕФЫЎЗбУПЖж5дЊЃЛЃЈ2ЃЉгІНЩФЩЫЎЗб47дЊ.
ЁОНтЮіЁП
ЃЈ1ЃЉЩшдкЯоЖЈСПвдФкУПЖжxдЊЃЌГЌГіВПЗжЕФЫЎЗбУПЖжyдЊ.ИљОн2дТЗнКЭ3дТЗнЕФНЩЗбЧщПіСаГіxКЭyЕФЖўдЊвЛДЮЗНГЬзщЃЌЧѓГіxКЭyЕФжЕМДПЩЃЛ
ЃЈ2ЃЉжБНгРћгУЃЈ1ЃЉжаНсЙћЧѓГіД№АИМДПЩЃЎ
(1)ЩшдкЯоЖЈСПвдФкУПЖжxдЊЃЌГЌГіВПЗжЕФЫЎЗбУПЖжyдЊ.
вРЬтвтЕУЃК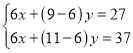
НтЕУ![]()
вђДЫдкЯоЖЈСПвдФкУПЖж2дЊЃЌГЌГіВПЗжЕФЫЎЗбУПЖж5дЊ.
ЃЈ2ЃЉ13-6=7(Жж)ЃЌ 6ЁС2+7ЁС5=47(дЊ)ЃЌ
вђДЫгІНЩФЩЫЎЗб47дЊ.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
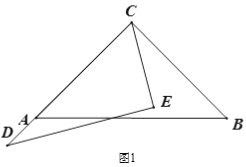
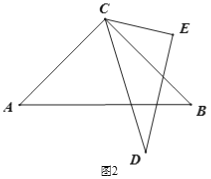
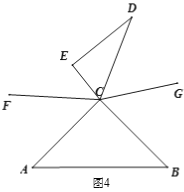
ЁОЬтФПЁПвбжЊНЋвЛИБШ§НЧАх(жБНЧШ§НЧАхABCКЭжБНЧШ§НЧАхCDEЃЌЁЯACBЃН90ЁуЃЌЁЯECDЃН60Ёу)ШчЭМ1АкЗХЃЌЕуDЁЂAЁЂCдквЛЬѕжБЯпЩЯЃЌНЋжБНЧШ§НЧАхCDEШЦЕуCФцЪБеыЗНЯђзЊЖЏЃЌБфЛЏАкЗХШчЭМЮЛжУ.
(1) ШчЭМ2ЃЌЕБЁЯACDЮЊЖрЩйЖШЪБЃЌCBЧЁКУЦНЗжЁЯECDЃП
(2) ШчЭМ3ЃЌЕБШ§НЧАхCDEАкЗХдкЁЯACBФкВПЪБЃЌзїЩфЯпCFЦНЗжЁЯACEЃЌЩфЯпCGЦНЗжЁЯBCDЃЌШчЙћШ§НЧаЮCDEдкЁЯACBФкШЦЕуCШЮвтзЊЖЏЃЌЁЯFCGЕФЖШЪ§ЪЧЗёЗЂЩњБфЛЏЃПШчЙћВЛБфЃЌЧѓЦфжЕЃЛШчЙћБфЛЏЃЌЫЕУїРэгЩ.
(3) ШчЭМ4ЃЌЕБШ§НЧАхCDEзЊЕНЁЯACBЭтВПЪБЃЌЩфЯпCFЁЂCGШдШЛЗжБ№ЦНЗжЁЯACEЁЂЁЯBCDЃЌдка§зЊЙ§ГЬжаЃЌ(2)жаЕФНсТлЪЧЗёГЩСЂЃПШчЙћНсТлГЩСЂЃЌЧыЫЕУїРэгЩЃЛШчЙћВЛГЩСЂЃЌЧыаДГіФуЕФНсТлВЂИљОнЭМ4ЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпACЃКyЃН![]() x+2ЗжБ№НЛxжсКЭyжсгкAЃЌCСНЕуЃЌжБЯпBDЃКyЃНЉx+bЗжБ№НЛxжсКЭyжсгкBЃЌDСНЕуЃЌжБЯпACгыBDНЛгкЕуEЃЌЧвOAЃНOBЃЎ
x+2ЗжБ№НЛxжсКЭyжсгкAЃЌCСНЕуЃЌжБЯпBDЃКyЃНЉx+bЗжБ№НЛxжсКЭyжсгкBЃЌDСНЕуЃЌжБЯпACгыBDНЛгкЕуEЃЌЧвOAЃНOBЃЎ
ЃЈ1ЃЉЧѓжБЯпBDЕФНтЮіЪНКЭEЕФзјБъЃЎ
ЃЈ2ЃЉШєжБЯпyЃНxЗжБ№гыжБЯпACЃЌBDНЛгкЕуHКЭFЃЌЧѓЫФБпаЮECOFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
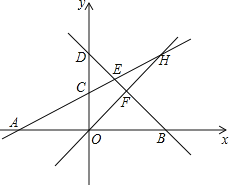
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌAЁЂBЮЊxжсЩЯСНЕуЃЌCЁЂDЮЊyжсЩЯЕФСНЕуЃЌОЙ§ЕуAЁЂCЁЂBЕФХзЮяЯпЕФвЛВПЗжc1гыОЙ§ЕуAЁЂDЁЂBЕФХзЮяЯпЕФвЛВПЗжc2зщКЯГЩвЛЬѕЗтБеЧњЯпЃЌЮвУЧАбетЬѕЗтБеЧњЯпГЩЮЊЁАЕАЯпЁБЃЎвбжЊЕуCЕФзјБъЮЊЃЈ0ЃЌЉ![]() ЃЉЃЌЕуMЪЧХзЮяЯпC2ЃКy=mx2Љ2mxЉ3mЃЈmЃМ0ЃЉЕФЖЅЕуЃЎ
ЃЉЃЌЕуMЪЧХзЮяЯпC2ЃКy=mx2Љ2mxЉ3mЃЈmЃМ0ЃЉЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЁАЕАЯпЁБдкЕкЫФЯѓЯоЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУЁїPBCЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЁїPBCУцЛ§ЕФзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЁїBDMЮЊжБНЧШ§НЧаЮЪБЃЌЧѓmЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
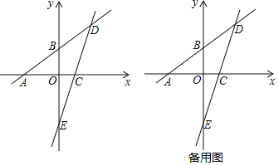
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌвЛДЮКЏЪ§y=![]() x+3ЕФЭМЯѓЗжБ№гыxжсЁЂyжсЯрНЛгкЕуAЁЂBЃЌЧвгыОЙ§ЕуC(2ЃЌ0)ЕФвЛДЮКЏЪ§y=kx+bЕФЭМЯѓЯрНЛгкЕуDЃЌЕуDЕФКсзјБъЮЊ4ЃЌжБЯпCDгыyжсЯрНЛгкЕуEЃЎ
x+3ЕФЭМЯѓЗжБ№гыxжсЁЂyжсЯрНЛгкЕуAЁЂBЃЌЧвгыОЙ§ЕуC(2ЃЌ0)ЕФвЛДЮКЏЪ§y=kx+bЕФЭМЯѓЯрНЛгкЕуDЃЌЕуDЕФКсзјБъЮЊ4ЃЌжБЯпCDгыyжсЯрНЛгкЕуEЃЎ
(1)жБЯпCDЕФКЏЪ§БэДяЪНЮЊ______ЃЛ(жБНгаДГіНсЙћ)
(2)дкxжсЩЯЧѓвЛЕуPЪЙЁїPADЮЊЕШбќШ§НЧаЮЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФЕуPЕФзјБъЃЎ
(3)ШєЕуQЮЊЯпЖЮDEЩЯЕФвЛИіЖЏЕуЃЌСЌНгBQЃЎЕуQЪЧЗёДцдкФГИіЮЛжУЃЌНЋЁїBQDбизХжБЯпBQЗелЃЌЪЙЕУЕуDЧЁКУТфдкжБЯпABЯТЗНЕФyжсЩЯЃПШєДцдкЃЌЧѓЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхвЛжжЖде§ећЪ§nЕФЁАFЁБдЫЫуЃКЂйЕБnЮЊЦцЪ§ЪБЃЌFЃЈnЃЉЃН3n+1ЃЛЂкЕБnЮЊХМЪ§ЪБЃЌFЃЈnЃЉ![]() ЃЈЦфжаkЪЧЪЙFЃЈnЃЉЮЊЦцЪ§ЕФе§ећЪ§ЃЉЁЁЃЌСНжждЫЫуНЛЬцжиИДНјааЃЌР§ШчЃЌШЁnЃН13ЃЌдђЃК
ЃЈЦфжаkЪЧЪЙFЃЈnЃЉЮЊЦцЪ§ЕФе§ећЪ§ЃЉЁЁЃЌСНжждЫЫуНЛЬцжиИДНјааЃЌР§ШчЃЌШЁnЃН13ЃЌдђЃК ШєnЃН24ЃЌдђЕк100ДЮЁАFЁБдЫЫуЕФНсЙћЪЧ________ЃЎ
ШєnЃН24ЃЌдђЕк100ДЮЁАFЁБдЫЫуЕФНсЙћЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєХзЮяЯпLЃКy=ax2+bx+cЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌabcЁй0ЃЉгыжБЯпlЖМОЙ§yжсЩЯЕФЭЌвЛЕуЃЌЧвХзЮяЯпLЕФЖЅЕудкжБЯпlЩЯЃЌдђГЦДЮХзЮяЯпLгыжБЯпlОпгаЁАвЛДјвЛТЗЁБЙиЯЕЃЌВЂЧвНЋжБЯпlНазіХзЮяЯпLЕФЁАТЗЯпЁБЃЌХзЮяЯпLНазіжБЯпlЕФЁАДјЯпЁБЃЎ
ЃЈ1ЃЉШєЁАТЗЯпЁБlЕФБэДяЪНЮЊy=2xЉ4ЃЌЫќЕФЁАДјЯпЁБLЕФЖЅЕуЕФКсзјБъЮЊЉ1ЃЌЧѓЁАДјЯпЁБLЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћХзЮяЯпy=mx2Љ2mx+mЉ1гыжБЯпy=nx+1ОпгаЁАвЛДјвЛТЗЁБЙиЯЕЃЌЧѓmЃЌnЕФжЕЃЛ
ЃЈ3ЃЉЩшЃЈ2ЃЉжаЕФЁАДјЯпЁБLгыЫќЕФЁАТЗЯпЁБlдкyжсЩЯЕФНЛЕуЮЊAЃЎвбжЊЕуPЮЊЁАДјЯпЁБLЩЯЕФЕуЃЌЕБвдЕуPЮЊдВаФЕФдВгыЁАТЗЯпЁБlЯрЧагкЕуAЪБЃЌЧѓГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЌЪБХзжРAЃЌBСНИіОљдШЕФаЁСЂЗНЬх(УПИіУцЩЯЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6)ЃЌЩшСНСЂЗНЬхГЏЩЯЕФЪ§зжЗжБ№ЮЊxЃЌyЃЌВЂвдДЫШЗЖЈЕуP(xЃЌy)ЃЌФЧУДЕуPТфдкжБЯпyЃНЃ2xЃЋ9ЩЯЕФИХТЪЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕу![]() дкЪ§жсЩЯЖдгІЕФЪ§ЮЊ
дкЪ§жсЩЯЖдгІЕФЪ§ЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЖдгІЕФЪ§ЮЊ
ЖдгІЕФЪ§ЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() жЎМфЕФОрРыМЧзїAB.
жЎМфЕФОрРыМЧзїAB.
![]()
вбжЊa=-2ЃЌbБШaДѓ12ЃЌ(1)дђBЕуБэЪОЕФЪ§ЪЧ_____ЃЛ
(2)ЩшЕу![]() дкЪ§жсЩЯЖдгІЕФЪ§ЮЊ
дкЪ§жсЩЯЖдгІЕФЪ§ЮЊ![]() ЃЌЕБPA-PB=4ЪБЃЌЧѓ
ЃЌЕБPA-PB=4ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(3)ШєЕуMвдУПУы1ИіЕЅЮЛЕФЫйЖШДгAЕуГіЗЂЯђгвдЫЖЏЃЌЭЌЪБЕуNвдУПУы2ИіЕЅЮЛЕФЫйЖШДгBЕуЯђзѓдЫЖЏЁЃЩшдЫЖЏЪБМфЪЧtУыЃЌдђдЫЖЏtУыКѓЃЌ
гУКЌtЕФДњЪ§ЪНБэЪОMЕуЕНДяЕФЮЛжУБэЪОЕФЪ§ЮЊ_____, NЕуЕНДяЕФЮЛжУБэЪОЕФЪ§ЮЊ_____ЃЛ
ЕБtЮЊЖрЩйУыЪБЃЌMгыNжЎМфЕФОрРыЪЧ9ЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com