
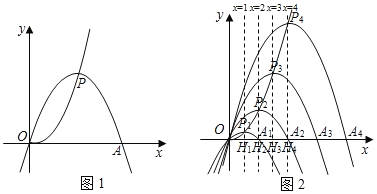
【题目】已知点P为抛物线y![]() x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
(1)①当△OPA为直角三角形时,m= ;
②当△OPA为等边三角形时,求此时“yp”的解析式;
(2)若P点的横坐标分别为1,2,3,…n(n为正整数)时,抛物线“yp”分别记作“![]() ”、“
”、“![]() ”…,“
”…,“![]() ”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
1)① Pn的坐标为 ;OAn= ;(用含n的代数式来表示)
②当PnHn﹣OAn=16时,求n的值.
2)是否存在这样的An,使得∠OP4An=90°,若存在,求n的值;若不存在,请说明理由.
【答案】(1)① 2;② y![]() x2+2
x2+2![]() x;(2)1):① (n,
x;(2)1):① (n,![]() n2);2n;② n=8;2):存在,n=10.
n2);2n;② n=8;2):存在,n=10.
【解析】
(1)①由△OPA为直角三角形时.得到△OPA为以点P为顶点的等腰直角三角形,从而可得答案,②由△OPA为等边三角形,过P作![]() 于
于![]() ,利用三角函数与抛物线的解析式
,利用三角函数与抛物线的解析式![]() ,求点
,求点![]() 的坐标,从而可得答案,
的坐标,从而可得答案,
(2)1)①利用Pn的横坐标为n,结合抛物线的对称性可得答案,②由 PnHn﹣OAn=16,建立方程求解即可,2) 画出图形,证明Rt△OP4H4∽Rt△P4AnH4即可得到答案.
解:(1)①当△OPA为直角三角形时.
∵PO=PA,故△OPA为以点P为顶点的等腰直角三角形,
∴点P的横坐标和纵坐标相同,故点P(m,m),
将点P的坐标代入y![]() x2得:m
x2得:m![]() m2,解得:m=0或2(舍去0).
m2,解得:m=0或2(舍去0).
故答案为:2;
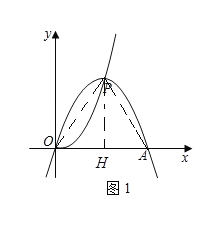
②当△OPA为等边三角形时,如图,过P作![]() 于
于![]() ,
,
![]()
![]()
![]() P(m,
P(m,![]() m),
m),
将点P的坐标代入抛物线表达式![]() ,
,
解得:m=2![]() ,
,
故点P的坐标为(2![]() ,6),
,6),
故“yp”的解析式为:y=a(x﹣2![]() )2+6,
)2+6,
点A的坐标为(2m,0),即(4![]() ,0),
,0),
将点A的坐标代入y=a(x﹣2![]() )2+6并解得:a
)2+6并解得:a![]() ,
,
故“yp”的解析式为:y![]() (x﹣2
(x﹣2![]() )2+6
)2+6![]() x2+2
x2+2![]() x;
x;
(2)1)① 由题意得:Pn的横坐标为n,则其坐标为(n,![]() n2),
n2),
由抛物线的对称性得:An=2n.
故答案为:(n,![]() n2);2n;
n2);2n;
②由题意得:PnHn﹣OAn![]() n2﹣2n=16,
n2﹣2n=16,
解得:n=8或﹣4(舍去﹣4),
∴n=8;
2)存在,理由:
如下图所示,由1)知,点P4的坐标为(4,8),An=2n,
即OH4=4,P4H4=8,H4An=2n﹣4,
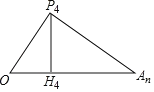
∵∠OP4An=90°,∴∠OP4H4+∠H4P4An=90°.
∵∠H4P4An+∠P4AnH4=90°,
∴∠OP4H4=∠P4AnH4,
∴Rt△OP4H4∽Rt△P4AnH4,
![]()
∴P4H42=OH4H4An,
即82=4×(2n﹣4),
解得:n=10.
![]() 当img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/03/d07c1de6/SYS202007220309563219592517_DA/SYS202007220309563219592517_DA.015.png" width="44" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />时,使得∠
当img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/03/d07c1de6/SYS202007220309563219592517_DA/SYS202007220309563219592517_DA.015.png" width="44" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />时,使得∠![]() =90°.
=90°.


科目:初中数学 来源: 题型:
【题目】已知![]() 中
中![]() 点
点![]() 分别在边
分别在边![]() 、边
、边![]() 上,连接
上,连接![]() 点
点![]() 、点
、点![]() 在直线
在直线![]() 同侧,连接
同侧,连接![]() 且
且![]() .
.
(1)点![]() 与点
与点![]() 重合时,
重合时,
①如图1,![]() 时,
时,![]() 和
和![]() 的数量关系是 ;位置关系是 ;
的数量关系是 ;位置关系是 ;
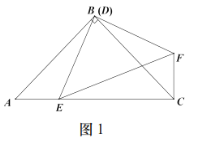
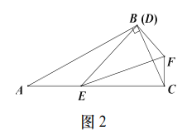
②如图2,![]() 时,猜想
时,猜想![]() 和
和![]() 的关系,并说明理由;
的关系,并说明理由;
(2)![]() 时,
时,
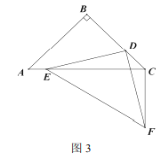
③如图3,![]() 时,若
时,若![]() 求
求![]() 的长度;
的长度;
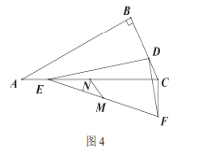
④如图4,![]() 时,点
时,点![]() 分别为
分别为![]() 和
和![]() 的中点,若
的中点,若![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确的有( )个.
,1),下列结论:①abc<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确的有( )个.
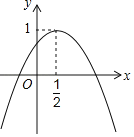
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件8元,出厂价为每件10元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3410元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小猪佩奇随机坐到![]() 座位的概率是________;
座位的概率是________;
(2)若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)求y与x之间的函数关系式.
(2)由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直l1∥l2,点A、B固定在直线l2上,点C是直线11上一动点,若点E、F分别为CA、CB中点,对于下列各值:①线段EF的长;②△CEF的周长;③△CEF的面积;④∠ECF的度数,其中不随点C的移动而改变的是( )

A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某百果园店售卖赣南脐橙,已知每千克脐橙的成本价为![]() 元,在销售脐橙的这
元,在销售脐橙的这![]() 天时间内,销售单价
天时间内,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数),日销售量
为整数),日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数)
为整数)
(1)请你直接写出日销售利润![]() (元)与时间第
(元)与时间第![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)该店有多少天日销售利润不低于![]() 元?
元?
(3)在实际销售中,该店决定每销售![]() 千克脐橙,就捐赠
千克脐橙,就捐赠![]() 元给希望工程,在这
元给希望工程,在这![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
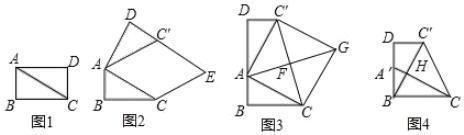
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如 图 1,将:矩形纸片 ABCD 沿对角线 AC 剪开,得到△ABC 和△ACD.并且量得 AB =4cm,AC=8cm.
操作发现:
(1)将图 1 中的△ACD 以点 A 为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到如图 2 所示的△AC′D,过点 C 作 AC′的平行线,与 DC'的延长线 交于点 E,则四边形 ACEC′的形状是 .
(2)创新小组将图 1 中的△ACD 以点 A 为旋转中心,按逆时针方向旋转,使 B、 A、D 三点在同一条直线上,得到如图 3 所示的△AC′D,连接 CC',取 CC′的中 点 F,连接 AF 并延长至点 G,使 FG=AF,连接 CG、C′G,得到四边形 ACGC′, 发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC 沿着 BD 方向平移,使点 B 与点 A 重合,此时 A 点平移至 A'点,A'C 与 BC′相交于点 H, 如图 4 所示,连接 CC′,试求 tan∠C′CH 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com