
如图所示:Rt△ABO中,直角边BO落在x轴负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1∶2,把△ABO缩小,则点A的对应点A′的坐标为__ ▲ .
科目:初中数学 来源: 题型:
 勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是
勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是查看答案和解析>>
科目:初中数学 来源: 题型:044
已知:如图所示,AB是⊙O的直径,P是AB上的一点(与A、B不重合),QP⊥AB,垂足为P,直线QA交⊙O于C点,过C点作⊙O的切线交直线QP于点D,则△CDQ是等腰三角形.对上述命题证明如下:

证明:连接OC.
∵OA=OC,
∴∠A=∠1.
∵CD切⊙O于C点,
∴∠OCD=90°.
∴∠1+∠2=90°.
∴∠A+∠2=90°.
在Rt△QPA中,∠QPA=90°,
∴∠A+∠Q=90°.
∴∠2=∠Q.∴DQ=DC.
即△CDQ是等腰三角形
问题:对上述命题,当点P在BA的延长线上时,其他条件不变,结论“△CDQ是等腰三角形”还成立吗?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:044
(2005 福州)已知:如图所示,AB是⊙O的直径,P是AB上的一点(与A、B不重合),QP⊥AB,垂足为P,直线QA交⊙O于C点,过C点作⊙O的切线交直线QP于点D,则△CDQ是等腰三角形,对上述命题证明如下:

证明 连接OC.∵OA=OC=OC,∴∠A==∠1.
∵CD切⊙O于C点,∴∠OCD=90=90°,
∴∠1+∠2=90°,∴∠A+∠2=90°,
在Rt△QPA中,∠QPA=90=90°,
∴∠A+∠Q=90=90°,∴∠2=∠Q.∴DQ=DC=DC.
即△CDQ是等腰三角形.
问题 对上述命题,当点P在BA的延长线上时,其他条件不变,如图所示,结论“△CDQ是等腰三角形”还成立吗?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
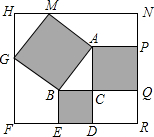 勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是________.
勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是________.查看答案和解析>>
科目:初中数学 来源:专项题 题型:填空题
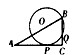
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com