
����Ŀ��Ϊ�˼�ǿѧУ���������ijѧУ�ƻ������ס��������������г����з��֣��������������2����������3������270Ԫ������������3����������2������230Ԫ��
��1����ס�����������ÿ�����ۼ۷ֱ��Ƕ���Ԫ��
��2��Ϊ���㿪չ�����������ѧУ�ƻ������ס�����������100�������ڹ��������̳�Э�̣��̳������������Ծ��۳��ۣ����������۳��ۣ�ѧУҪ����������������������������������4�����������������������90�����������ѧУ������Ǯ�Ľ���������
��3��ѧУ���ó�ʡ�µ�290Ԫ������������������������ģ�����10Ԫһ�������5Ԫһ�����ڰ�Ǯ�þ�������£��ж����ֽ���������
���𰸡���1����������ÿ�����ۼ�Ϊ30Ԫ����������ÿ�����ۼ�Ϊ70Ԫ����2��������Ǯ�Ľ�������Ϊ������������90������������10������3����28�ֽ���������
��������
��1��������������г���Ӧ�ķ����飬�Ӷ����Խ���⣻
��2����ѧУ�ƻ�������������m������ѧУ�ƻ�������������100m���������������в���ʽ���ɵõ����ۣ�
��3���蹺������a�������b������������÷���10a��5b��290�����b��582a��0���ⲻ��ʽ���ɵõ����ۣ���
��1�����������ÿ�����ۼ�Ϊ![]() Ԫ����������ÿ�����ۼ�Ϊ
Ԫ����������ÿ�����ۼ�Ϊ![]() Ԫ�������⣬��
Ԫ�������⣬��
![]() ���
���![]()
�𣺼�������ÿ�����ۼ�Ϊ30Ԫ����������ÿ�����ۼ�Ϊ70Ԫ��
��2����ѧУ������������![]() ��������������
��������������![]() ����
����
����֪����![]() .���
.���![]() ��
��
��![]() ����
����![]() ��
��
�蹺���ס�����������ѧУ����ǮΪ![]() Ԫ��
Ԫ��
��![]() ��
��
����![]() ʱ��
ʱ��![]() ȡ��Сֵ��������ǮΪ2990Ԫ��������Ǯ�Ľ�������Ϊ������������90������������10����
ȡ��Сֵ��������ǮΪ2990Ԫ��������Ǯ�Ľ�������Ϊ������������90������������10����
��3���蹺������![]() �������
�������![]() ������
������![]() ��
��![]() ��
��
���![]() ��
��
��![]() ��������
��������
����28�ֽ���������


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ӿȪ�����й����۽�֮�磬��֪ij�۽���ֲ���ү���۽۳ɱ�Ϊ2Ԫ/ǧ�ˣ������δ��90���۽۵����۵���p��Ԫ/ǧ�ˣ���ʱ��t���죩֮��ĺ�����ϵʽΪp=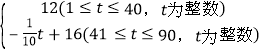 �����۽۵�������y��ǧ�ˣ���ʱ��t���죩����һ�κ�����ϵ���䲿���������±���ʾ��
�����۽۵�������y��ǧ�ˣ���ʱ��t���죩����һ�κ�����ϵ���䲿���������±���ʾ��
ʱ��t/�� | 1 | 10 | 20 | 40 | 70 | 90 |
��������y/ǧ�� | 105 | 150 | 200 | 300 | 450 | 550 |
��1����y��t֮��ĺ�������ʽ��
��2����δ��90��������У�Ԥ����һ�����������������������������Ϊ����Ԫ��
��3����ʵ�����۵ĺ�50���У����ү����ÿ����1ǧ���۽۾;���nԪ����n��5�������ض�ͯ��Ϊ��ѧ�����۹����з��ү���֣�ǡ�ôӵ�51�쿪ʼ����ǰһ����ȣ��۳���������������������ռ��٣������n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y����a��1��x2+3ax+1ͼ���ϵ��ĸ��������Ϊ��x1��m������x2��m������x3��n������x4��n��������m��n�����н��ۿ�����ȷ���ǣ�������
A.��a��![]() ���� x1��x2��x3��x4
���� x1��x2��x3��x4
B.��a��![]() ���� x4��x1��x2��x3
���� x4��x1��x2��x3
C.��a����![]() ���� x1��x3��x2��x4
���� x1��x3��x2��x4
D.��a����![]() ���� x3��x2��x1��x4
���� x3��x2��x1��x4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��mx2��2mx+n(m��0)��x�ύ�ڵ�A��B����A������Ϊ(��2��0)��
(1)д�������ߵĶԳ��
(2)ֱ��![]() ����B�����������ߵ���һ������ΪC��
����B�����������ߵ���һ������ΪC��
�ٷֱ���ֱ�ߺ�����������Ӧ�ĺ�������ʽ��
�ڵ�PΪ�����߶Գ����ϵĶ��㣬����P������ֱ��l1��y��x+a��l2��y����x+b���ͼ��G����ͼ��G���߶�BC�й�����ʱ��ֱ��д����P��������t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
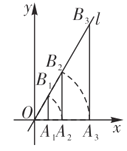
����Ŀ����ͼ����![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��![]() ��Ĵ��߽���ԭ����
��Ĵ��߽���ԭ����![]() ��н�Ϊ
��н�Ϊ![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����ԭ��
����ԭ��![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶������
�ij�Ϊ�뾶������![]() ���������ڵ�
���������ڵ�![]() ���ٹ���
���ٹ���![]() ��
��![]() ��Ĵ��߽�ֱ��
��Ĵ��߽�ֱ��![]() �ڵ�
�ڵ�![]() ����ԭ��
����ԭ��![]() ΪԲ�ģ���
ΪԲ�ģ���![]() �ij�Ϊ�뾶������
�ij�Ϊ�뾶������![]() ���������ڵ�
���������ڵ�![]() ������������������ȥ�����
������������������ȥ�����![]() ��������_____��
��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
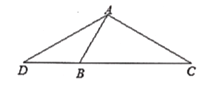
����Ŀ����ͼ����֪����������![]() ���߶�
���߶�![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ������
������![]() .
.
��1����![]() ����
����![]() �ij���
�ij���
��2����![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
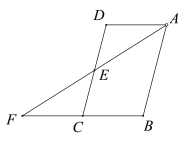
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�E��CD���е㣬����AE���ӳ���BC���ӳ����ڵ�F
��1����֤����ADE�ա�FCE��
��2����AB=2AD����F��30�������FAB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
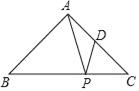
����Ŀ����ͼ���ڵ���ֱ��������ABC�У�AB��AC��2����BAC��90�㣬��D��AC���е㣬��P��BC���ϵĶ��㣬����PA��PD����PA+PD����СֵΪ��������
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����7�֣���У�ֻ�������Խ��Խ�ܵ����Ĺ�ע��С�����������������ijУ����ѧ���ͼҳ�����ѧ�����ֻ�����Ŀ��������������µ�ͳ��ͼ��
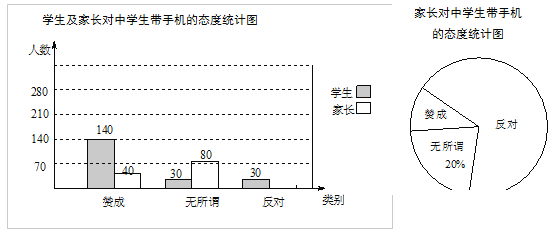
��1������ε����������������ȫͼ1��
��2����ͼ2�б�ʾ�ҳ���������Բ�ĽǵĶ�����
��3��������������������������ӳ���һ���ʾ�ɵ�4λ�ҳ������ѡ��2λ����������飬���а���С����С���ļҳ�������������״ͼ���б��ķ��������С����С���ļҳ���ͬʱѡ�еĸ�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com