
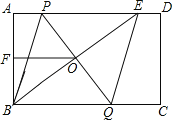
【题目】如图,在矩形ABCD中,E是AD边上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、QE
(1)求证:四边形BPEQ是菱形:
(2)若AB=6,F是AB中点,OF=4,求菱形BPEQ的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
(2)先证明OF为△BAE的中位线,然后依据三角形的中位线定理得出AE∥OF且OF=![]() AE.求得OB的长,则可得到BE的长,设菱形的边长为x,则AP=8﹣x,在Rt△APB中依据勾股定理可列出关于x的方程,然后依据菱形的面积公式进行计算即可.
AE.求得OB的长,则可得到BE的长,设菱形的边长为x,则AP=8﹣x,在Rt△APB中依据勾股定理可列出关于x的方程,然后依据菱形的面积公式进行计算即可.
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,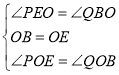 ,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)解:∵AB=6,F是AB的中点,
∴BF=3.
∵四边形BPEQ是菱形,
∴OB=OE.
又∵F是AB的中点,
∴OF是△BAE的中位线,
∴AE∥OF且OF=![]() AE.
AE.
∴∠BFO=∠A=90°.
在Rt△FOB中,OB=![]() =5,
=5,
∴BE=10.
设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,BP2=AB2+AP2,
即x2=62+(8﹣x)2,
解得:x=![]() ,
,
∴BQ=![]() ,
,
∴菱形BPEQ的面积=BQ×AB=![]() ×6=
×6=![]() .
.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
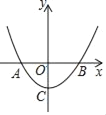
【题目】如图,二次函数y=x2﹣m2(m>0且为常数)的图象与x轴交于点A、B(A在B左侧),与y轴交于C.
(1)求A,B,C三点的坐标(用含m的式子表示);
(2)若∠ACB=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
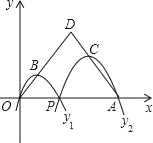
【题目】如图,已知点A(12,0),O为坐标原点,P是线段OA上任一点(不含端点O、A),二次函数y1的图象过P、O两点,二次函数y2的图象过P、A两点,它们的开口均向下,顶点分别为B、C,射线OB与射线AC相交于点D.则当OD=AD=9时,这两个二次函数的最大值之和等于( )
A. 8 B. 3![]() C. 2
C. 2![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形![]() 中,动点
中,动点![]() 从
从![]() 点出发,以每秒1个单位长度的速度沿
点出发,以每秒1个单位长度的速度沿![]() 向
向![]() 点运动,同时动点
点运动,同时动点![]() 从
从![]() 点出发,以每秒2个单位长度的速度沿
点出发,以每秒2个单位长度的速度沿![]() 方向运动,当
方向运动,当![]() 运动到
运动到![]() 点时,
点时,![]() 、
、![]() 两点同时停止运动.设
两点同时停止运动.设![]() 点运动的时间为
点运动的时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数关系的图象是( )
的函数关系的图象是( )

A.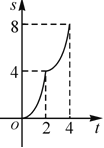 B.
B.
C.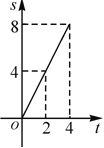 D.
D.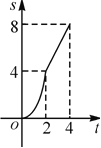
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,E是BC边上一点,将矩形沿AE折叠,点B落在点B'处,当△B'EC是直角三角形时,BE的长为( )
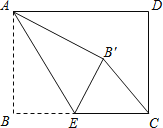
A.2B.6C.3或6D.2或3或6
查看答案和解析>>
科目:初中数学 来源: 题型:
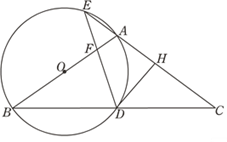
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若![]() ,求证:A为EH的中点.
,求证:A为EH的中点.
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
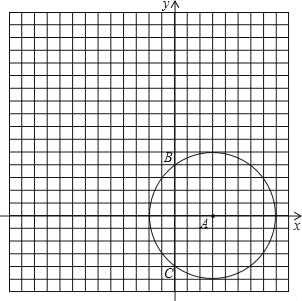
【题目】如图,正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系,圆心为 A(3,0)的⊙A被y轴截得的弦长BC=8.
解答下列问题:
(1)求⊙A 的半径;
(2)请在图中将⊙A 先向上平移 6 个单位,再向左平移8个单位得到⊙D,并写出圆心D的坐标;
(3)观察你所画的图形,对⊙D 与⊙A 的位置关系作出合情的猜想,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
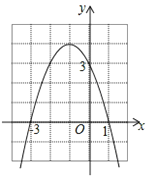
【题目】如图所示是二次函数y=ax2+bx+c的图象.下列结论:①二次三项式ax2+bx+c的最大值为4;②使y≤3成立的x的取值范围是x≤-2;③一元二次方程ax2+bx+c=1的两根之和为-1;④该抛物线的对称轴是直线x=-1;⑤4a-2b+c<0.其中正确的结论有______________.(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了处理污水需要铺设一条长为2000米的管道,实际施工时,×××××××,设原计划每天铺设管道![]() 米,则可列方程
米,则可列方程![]() ,根据此情景,题目中的“×××××××”表示所丢失的条件,这一条件为( )
,根据此情景,题目中的“×××××××”表示所丢失的条件,这一条件为( )
A.每天比原计划多铺设10米,结果延期10天完成任务
B.每天比原计划少铺设10米,结果延期10天完成任务
C.每天比原计划少铺设10米,结果提前10天完成任务
D.每天比原计划多铺设10米,结果提前10天完成任务
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com