
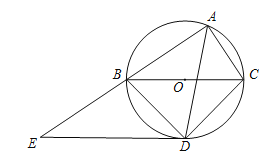
【题目】如图,⊙O是Rt△ABC的外接圆,∠BAC=90°,AD平分∠BAC,且交⊙O于点D,过点D作DE∥BC,交AB的延长线于点E,连接BD、CD.
(1)求证:DE是⊙O的切线;
(2)若AB=8,AC=6,求BE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,根据圆周角定理求得∠COD=2∠DAC=90°,∠BOD=2∠BAD=90°,再根据平行线的性质可求OD⊥ED,即可证得DE是⊙O的切线;
(2)根据勾股定理求得BC的长,从而求得OB的长,然后求得BD、CD的长,再根据边形ABCD是⊙O的内接四边形,求得∠ACD=∠DBE,再证得△EBD∽△DCA,得到![]() ,由此求得BE的长.
,由此求得BE的长.
(1)证明:连接OD.
∵∠BAC=90°,AD平分∠BAC,∴∠BAD=∠DAC=![]() ∠BAC=45°.
∠BAC=45°.
∴∠COD=2∠DAC=90°.
∠BOD=2∠BAD=90°.
∵DE∥BC,∴∠COD=∠EDO=90°.
∵∠EDO=90°,∴OD⊥ED.
∵OD为半径,OD⊥ED,垂足为点D,∴DE是⊙O的切线.
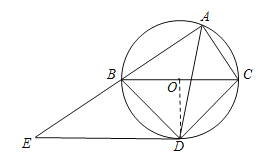
(2)解:∵∠BAC=90°,∴BC是⊙O的直径.
在Rt△BAC中,∠BAC=90°,BC= ![]() =10 ,∴OB=OC=OD=5.
=10 ,∴OB=OC=OD=5.
∵OB=OD=5,∴∠OBD=∠ODB=![]() (180°-∠BOD)=45°.
(180°-∠BOD)=45°.
∴∠BDE=∠EDO-∠ODB=45°.
在Rt△BOD中,∠BOD=90°,BD= ![]() .
.
在Rt△DOC中,∠COD=90°,CD=![]() .
.
∵四边形ABCD是⊙O的内接四边形,∴∠ACD+∠ABD=180°.
又∵∠EBD+∠ABD=180°,∴∠ACD=∠DBE.
∵∠ACD=∠EBD,∠BDE=∠DAC=45°,∴△EBD∽△DCA.
∴![]() .
.
∴![]() .
.
∴EB=![]() .
.
答:BE的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课余生活,拓展学生的视野,某学校开设了特色选修课程.本学期该校共开设A、B、C三类课程,如下表所示.

(1)若小明从A类课程中随机选择一门课程,则他恰好选中“合唱”的概率是 .
(2)若小明分别从B类课程和C类课程中各随机选择一门课程,求他恰好选中“汉字的故事”和“乒乓球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 ,x2 ,且x12+x22=10,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
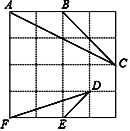
【题目】如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
⑴填空:∠ABC= °,AC= ;
⑵判断:△ABC与△DEF是否相似,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=![]() 的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.
的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为(3,5),(6,1).若过原点的直线l将这个图案分成面积相等的两部分,则直线l的函数解析式为_____.
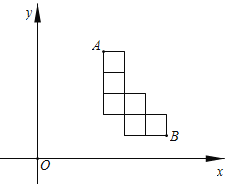
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com