
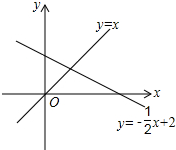
 已知平行于y轴的直线x=t,与直线y=x和直线y=-$\frac{1}{2}$x+2分别交于点D、E(E在D的上方).
已知平行于y轴的直线x=t,与直线y=x和直线y=-$\frac{1}{2}$x+2分别交于点D、E(E在D的上方).分析 将x=t代入解析式,得到y与t的关系式,然后根据直线在y轴的左侧和在y轴的右侧两种情况并以不同边为斜边构造等腰直角三角形,根据等腰直角三角形的性质求出t的值,进而求出各点坐标.
解答 解:当x=t时,y=x=t;
当x=t时,y=-$\frac{1}{2}$x+2=-$\frac{1}{2}$t+2.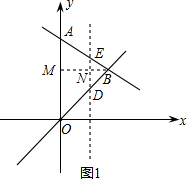
∴E点坐标为(t,-$\frac{1}{2}$t+2),D点坐标为(t,t).
∵E在D的上方,
∴DE=-$\frac{1}{2}$t+2-t=-$\frac{3}{2}$t+2,且t<$\frac{4}{3}$.
∵△PDE为等腰直角三角形,
∴PE=DE或PD=DE或PE=PD.
若t>0,PE=DE时,-$\frac{3}{2}$t+2=t,
∴t=$\frac{4}{5}$,-$\frac{1}{2}$t+2=$\frac{8}{5}$,
∴P点坐标为(0,$\frac{8}{5}$).
若t>0,PD=DE时,-$\frac{3}{2}$t+2=t,
∴t=$\frac{4}{5}$,
∴P点坐标为(0,$\frac{4}{5}$).
若t>0,PE=PD时,即DE为斜边,
∴-$\frac{3}{2}$t+2=2t
∴t=$\frac{4}{7}$,DE的中点坐标为(t,$\frac{1}{4}$t+1),
∴P点坐标为(0,$\frac{8}{7}$).
若t<0,PE=DE和PD=DE时,由已知得DE=-t,-$\frac{3}{2}$t+2=-t,t=4>0(不符合题意,舍去),
此时直线x=t不存在.
若t<0,PE=PD时,即DE为斜边,由已知得DE=-2t,-$\frac{3}{2}$t+2=-2t,
∴t=-4,$\frac{1}{4}$t+1=0,
∴P点坐标为(0,0).
综上所述:当t=$\frac{4}{5}$时,△PDE为等腰直角三角形,此时P点坐标为(0,$\frac{8}{5}$)或(0,$\frac{4}{5}$);
当t=$\frac{4}{7}$时,△PDE为等腰直角三角形,此时P点坐标为(0$\frac{8}{7}$);
当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0).
点评 此题难度很大,涉及变量较多,解答时需要将x转化为t,然后根据等腰三角形的性质进行推理,由于情况较多,容易造成漏解,故解答时要仔细.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{(-2)}^2}}=-2$ | B. | $\sqrt{3^2}=9$ | C. | $-\sqrt{9}=-3$ | D. | $\sqrt{-9}=-3$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com