
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
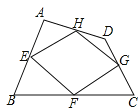
(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形.
(3)你学过的哪种特殊四边形的中点四边形是菱形? .
【答案】(1)平行四边形;(2)AC⊥BD;(3)矩形的中点四边形是菱形
【解析】解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图1,连结BD.
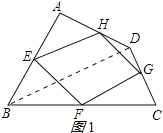
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
故答案为:平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图2,连结AC、BD.
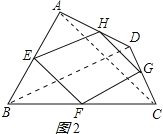
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案为:AC⊥BD;
(3)矩形的中点四边形是菱形.理由如下:
如图3,连结AC、BD.
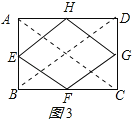
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH=![]() BD,FG=
BD,FG=![]() BD,EF=
BD,EF=![]() AC,GH=
AC,GH=![]() AC,
AC,
∵四边形ABCD是矩形,
∴AC=BD,∴EF=FG=GH=EH,
∴四边形EFGH是菱形.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左边到右边的变形,是因式分解的是( )
A. y2﹣2y+4=(y﹣2)2
B. 10x2﹣5x=5x(2x﹣1)
C. a(x+y)=ax+ay
D. t2﹣16+3t=(t+4)(t﹣4)+3t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】玩“24点”游戏,规则如下:任取4个整数,将这4个数(每个数只用1次)进行“+、-、×、÷”四则运算,使结果为24.现有4个整数:-13、-3、-2、3,应用上述规则,写出一个算式____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com