练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    不等式组：


    由①得x>1            

         

    由②得x<4           

    所以1<x<4         


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


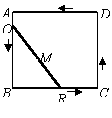
    如图,正方形ABCD的边长为2，将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动．如果Q点从A点出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时点R从B点出发，沿图中所示方向按B→C→D→A→B滑动到B止，在这个过程中，线段BM的长为线段        ，QR的中点M所经过的路线围成的图形的面积为                                  

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，BC=8，AB=6，经过点B和点D的两个动圆均与AC相切，且与AB、BC、  AD、DC分别交于点G、H、E、F，则EF+GH的最小值是（      ）

         A．6        B．8        C．9.6         D．10

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若关于x的一元二次方程有两个不相等的实数根，则的取值范围是（    ）

    A.       B. 且k≠1      C.        D. ≥且

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若补角是余角的3倍，则=            ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为了提倡低碳经济，某公司为了更好得节约能源，决定购买一批节省能源的10台新机器。现有甲、乙两种型号的设备，其中每台的价格、工作量如下表.。经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台甲型设备比购买3台乙型设备少6万元．

     

    甲型

    乙型

    价格（万元/台）

    产量（吨/月）

    240

    180

    （1）求a, b的值；

    （2）经预算：该公司购买的     节能设备的资金不超过110万元，请列式解答有几种购买方案可供 选择；

    （3）在（2）的条件下，若每月要求产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案 。    

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是由棱长为1的正方体搭成的三视图，则图中棱长为1的正方体的个数是…… (   )

    　      

    主视图　　   左视图　        俯视图

    A．3个              B．5个              C．6个            D．8个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，有三条线段AB、BD、DC， AB=6，BD=8，DC=2，且AB//DC。点E和点F分别为BD上的两个动点，且。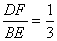

    （1）       求证：△ABE∽△CDF

    （2）       当EF=2时，求BE的长度

    （3）       在以上2个问题的解题过程中，概括（或者描述）你所用到数学基本知识（定义、定理等）或者是利用的数学思想方法。(共写出2点即可)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


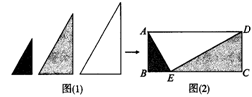
    如图（1）所示，用形状相同、大小不等的三块直角三角形木板，恰好能拼成如图（2）所示的四边形ABCD，若AE＝2，CE＝4BE，那么这个四边形的面积是            ．

    （第15题图）
     
     


    查看答案和解析>>

    同步练习册答案