
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把y系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把t系数化为1,即可求出解;
(5)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)移项合并得:6x=6,
解得:x=1;
(2)去分母得:12-2(2x-5)=3(3-x),
去括号得:12-4x+10=9-3x,
移项合并得:-x=-13,
解得:x=13;
(3)去分母得:10y-5(y+1)=20-2(y+2),
去括号得:10y-5y-5=20-2y-4,
移项得:10y-5y+2y=20-4+5,
合并同类项得:7y=21,
解得:y=3;
(4)去分母得,4(2t-6)-3(2t-4)=24,
去括号得,8t-24-6t+12=24,
移项得,8t-6t=24+24-12,
合并同类项得,2t=36,
系数化为1得,t=18
(5)整理,得$\frac{4x+9}{5}$-$\frac{3+2x}{3}$=$\frac{x-5}{2}$,
去分母,得6(4x+9)-10(3+2x)=15(x-5),
去括号,得24x+54-30-20x=15x-75,
移项,得24x-20x-15x=-75-54+30,
合并,得-11x=-99,
系数化为1,得x=9.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.


科目:初中数学 来源: 题型:填空题
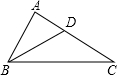 如图,在△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,AD=2,AB=2$\sqrt{3}$,那么S△ABC=6$\sqrt{3}$.
如图,在△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,AD=2,AB=2$\sqrt{3}$,那么S△ABC=6$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
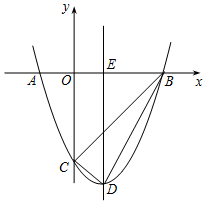 如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com