
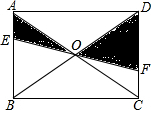
 如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形的面积为s,那么阴影部分的面积是$\frac{S}{4}$.
如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形的面积为s,那么阴影部分的面积是$\frac{S}{4}$. 分析 由△AOE≌△COF,可得S△AOE=S△COF,可得S阴=S△COD=$\frac{1}{4}$S矩形ABCD.
解答 解:∵四边形ABCD是矩形,
∴AB∥CD,OA=OC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF,
∴S△AOE=S△COF,
∴S阴=S△COD=$\frac{1}{4}$S矩形ABCD=$\frac{S}{4}$,
故答案为$\frac{s}{4}$
点评 本题考查矩形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形的条件解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
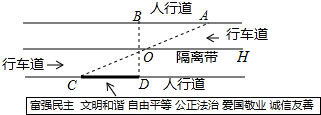 杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD,创设数学情境如下:
杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD,创设数学情境如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:
某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
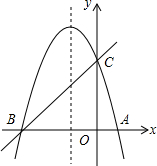 如图,已知抛物线y=-x2+bx+c的对称轴为直线x=-1,与y轴交于点C(0,3),与x轴交于点A和点B.
如图,已知抛物线y=-x2+bx+c的对称轴为直线x=-1,与y轴交于点C(0,3),与x轴交于点A和点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com