
分析 (1)用直接开平方法求解即可;
(2)用配方法求解;
(3)用因式分解法求解即可;
(4)用配方法求解即可;
(5)用因式分解法求解即可.
解答 解:(1)移项得:(x-2)2=4,
两边开方得:x-2=2或x-2=-2,
解得:x=4或x=0;
(2)移项得到x2-4x=3,
配方得:(x-2)2=7,
∴x-2=$\sqrt{7}$或x-2=-$\sqrt{7}$,
解得:x=2+$\sqrt{7}$或x=2-$\sqrt{7}$;
(3)移项得:3(x-2)2-x(x-2)=0,
提公因式得:(x-2)[3(x-2)-x]=0,
即:x-2=0或2x-6=0,
解得:x=2或x=3;
(4)移项得:x2+4x=5,
配方得:x2+4x+4=5+4,
即(x+2)2=9,
所以x+2=3或x+2=-3,
解得:x=1或x=-5;
(5)因式分解得:(x-$\sqrt{3}$)2=0.
解得:x1=x2=$\sqrt{3}$.
点评 考查了一元二次方程的解法,解题的关键是根据具体的题目选择合适的解方程的方法,难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
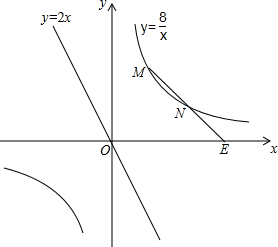 某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.
某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
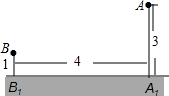 如图,大江的一侧有A、B两个工厂,它们有垂直于江边的小路,长度分别为3千米和1千米,设两条小路相距4千米,现在要在江边建立一个抽水站,把水送到A、B两厂去,欲使供水管路最短,抽水站应建在哪里?
如图,大江的一侧有A、B两个工厂,它们有垂直于江边的小路,长度分别为3千米和1千米,设两条小路相距4千米,现在要在江边建立一个抽水站,把水送到A、B两厂去,欲使供水管路最短,抽水站应建在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y是x的二次函数 | B. | 二次项系数是-10 | C. | 一次项是100 | D. | 常数项是20000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com