练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，一次函数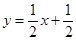的图象与x轴交于点A，与y轴交于点B，与反比例函数的图象在第一象限内交于点C，CD⊥x轴于点D，OD＝2AO，求反比例函数的表达式．

    .

    解析试题分析：根据已知，应用相似三角形的判定和性质以及曲线上点的坐标与方程的关系求出点C的坐标，代入即可求解.
    ∵一次函数的图象与x轴交于点A，与y轴交于点B ，
    ∴令，得；令，得.
    ∴点A坐标为，点B坐标为. ∴OA=1，OB=.
    ∵CD⊥x轴，∴CD//OB. △AOB∽△ADC. .
    ∵OD=2AO，. ∴CD=.
    ∴点C的纵坐标为.
    ∵点C在一次函数的图象上，∴点C的坐标为.
    ∴反比例函数的表达式 .
    考点：1.一次函数与反比例函数交点问题；2.曲线上点的坐标与方程的关系；3.相似三角形的判定和性质.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    关于x的函数y=（m2-1）x2-（2m+2）x+2的图象与x轴只有一个公共点，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    为了响应国家节能减排的号召，鼓励市民节约用电，我市从2012年7月1日起，居民用电实行“一户一表”的“阶梯电价”，分三个档次收费，第一档是用电量不超过180千瓦时实行“基本电价”，第二、三档实行“提高电价”，具体收费情况如图的折线图，请根据图象回答下列问题；
    (1)当用电量是180千瓦时时，电费是__________元；
    (2)第二档的用电量范围是__________；
    (3)“基本电价”是__________元/千瓦时；
    (4)小明家8月份的电费是328．5元，这个月他家用电多少千瓦时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在平面直角坐标系中，直线y＝2x＋b（b＜0）与坐标轴交于A，B两点，与双曲线（x>0）交于D点，过点D作DC⊥x轴，垂足为C，连接OD。已知△AOB≌△ACD。
    （1）如果b=－2，求k的值；
    （2）试探究k与b的数量关系，并写出直线OD的解析式。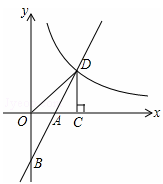

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知A、B两地相距300千米，甲、乙两车同时从A地出发，以各自的速度匀速往返两地，甲车先到达B地，停留1小时后按原路返回．设两车行驶的时间为x小时，离开A地的距离是y千米，如图是y与x的函数图象．
    (1)计算甲车的速度为   千米／时，乙车的速度为   千米／时；
    (2)几小时后两车相遇；
    (3)在从开始出发到两车相遇的过程中，设两车之间的距离为S千米，乙车行驶的时间为t小时，求S与t之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    某移动通讯公司开设了两种通讯业务：“全球通”使用者先缴50元月租费，然后每通话1分钟，再付话费0．4元；“神舟行”不缴月租费，每通话1min付费0．6元．若一个月内通话x min，两种方式的费用分别为y1元和y2元．
    （1）写出y1、y2与x之间的函数关系式；
    （2）一个月内通话多少分钟，两种移动通讯费用相同；
    （3）你能为用户设计一个方案，使用户合理地选择通信业务吗？
    （4）某人估计一个月内通话300min，应选择哪种移动通讯合算些．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在学习三角形中线的知识时，小明了解到：三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分。进而，小明继续研究，过四边形的某一顶点的直线能否将该四边形平分为面积相等的两部分？他画出了如下示意图（如图1），得到了符合要求的直线AF.

    小明的作图步骤如下：
    第一步：连结AC；
    第二步：过点B作BE//AC交DC的延长线于点E；
    第三步：取ED中点F，作直线AF；
    则直线AF即为所求.
    请参考小明思考问题的方法，解决问题：
    如图2，五边形ABOCD，各顶点坐标为：A(3,4)，B(0,2)，O(0,0)，C(4,0)，D(4,2).请你构造一条经过顶点A的直线，将五边形ABOCD分为面积相等的两部分，并求出该直线的解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    某公司有甲种原料260kg，乙种原料270kg，计划用这两种原料生产A、B两种产品共40件．生产每件A种产品需甲种原料8kg，乙种原料5kg，可获利润900元；生产每件B种产品需甲种原料4kg，乙种原料9kg，可获利润1100元．设安排生产A种产品x件．
    （1）完成下表

     
    		甲（kg）
    		乙（kg）
    		件数（件）
    A
    		 
    		5x
    		x
    B
    		4（40-x）
    		 
    		40-x
    （2）安排生产A、B两种产品的件数有几种方案？试说明理由；
    （3）设生产这批40件产品共可获利润y元，将y表示为x的函数，并求出最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，直线y=k1x+b（k1≠0）与双曲线（k2≠0）相交于A（1，m）、B（-2，-1）两点．求直线和双曲线的解析式．

    查看答案和解析>>

    同步练习册答案