
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与y轴交于点C,与反比例函数y=![]() 的图象交于A,B两点,过点B作BE⊥x轴于点E,已知A点坐标是(2,4),BE=2.
的图象交于A,B两点,过点B作BE⊥x轴于点E,已知A点坐标是(2,4),BE=2.
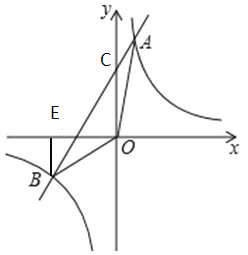
(1)求一次函数与反比例函数的表达式;
(2)连接OA、OB,求△AOB的面积.
【答案】(1)y=x+2, y=![]() ;(2)6.
;(2)6.
【解析】
(1)根据点A坐标将反比例函数表达式求出,再利用反比例函数求出点B的坐标,最后根据点A和点B坐标用待定系数法求出一次函数表达式;
(2)求出点C坐标,再根据S△AOB=S△BOC+S△AOC可得结果.
解:(1)∵点A(2,4)在反比例函数y=![]() 的图象上,
的图象上,
∴将A(2,4)代入y=![]() 中,可得4=
中,可得4=![]() ,解得m=8,即反比例函数表达式为y=
,解得m=8,即反比例函数表达式为y=![]() .
.
∵BE⊥x轴于点E,且BE=2,即点B纵坐标为-2,而点B在反比例函数y=![]() 的图象上,
的图象上,
∴将y=-2代入y=![]() ,
,
得-2=![]() ,解得x=-4.
,解得x=-4.
即点B坐标为(-4,-2),
∵点A(2,4),B(-4,-2)在一次函数y=kx+b的图象上,
∴将A(2,4),B(-4,-2)代入y=kx+b中,得![]() 解得
解得![]()
∴一次函数表达式为y=x+2,反比例函数表达式为y=![]() ;
;
(2)∵点C为一次函数y=x+2的图象与y轴的交点,
∴令x=0,得y=2,即C(0,2).
S△AOB=S△BOC+S△AOC
=![]() ·OC·|xB|+
·OC·|xB|+![]() ·OC·|xA|
·OC·|xA|
=![]() ·OC·|xA-xB|
·OC·|xA-xB|
=![]() ×2×6
×2×6
=6.


科目:初中数学 来源: 题型:
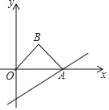
【题目】如图,直线y=![]() x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=
x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=![]() x﹣2上时,则△OAB平移的距离是_____.
x﹣2上时,则△OAB平移的距离是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
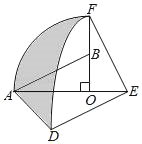
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分別以O、E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察猜想
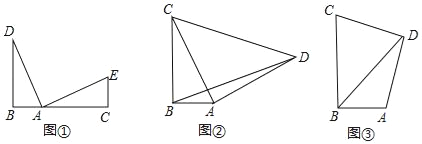
如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为;
(2)问题解决
如图②,在Rt△ABC中,∠ABC=90°,CB=4,AB=2,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;
(3)拓展延伸
如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=4,AB=2,DC=DA,请直接写出BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:折纸中的数学
问题背景
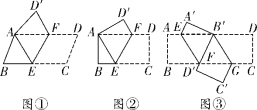
在数学活动课上,老师首先将平行四边形纸片ABCD按如图①所示方式折叠,使点C与点A重合,点D落到D′处,折痕为EF.这时同学们很快证得:△AEF是等腰三角形.接下来各学习小组也动手操作起来,请你解决他们提出的问题.
操作发现
(1) “争先”小组将矩形纸片ABCD按上述方式折叠,如图②,发现重叠部分△AEF恰好是等边三角形,求矩形ABCD的长、宽之比是多少?
实践探究
(2)“励志”小组将矩形纸片ABCD沿EF折叠,如图③,使B点落在AD边上的B′处;沿B′G折叠,使D点落在D′处,且B′D′过F点.试探究四边形EFGB′是什么特殊四边形?
(3)再探究:在图③中连接BB′,试判断并证明△BB′G的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
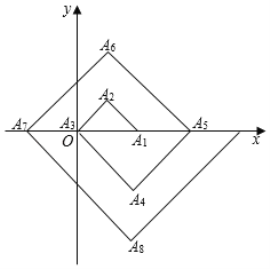
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com