
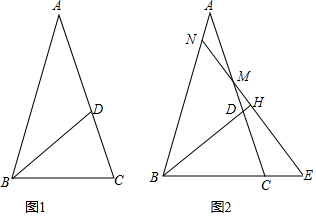
分析 (1)根据等腰三角形的性质得到∠A=∠DBA=∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠C,根据三角形的内角和即可得到结论;
(2)①根据已知条件得到∠ABD=∠CBD=36°,根据垂直的定义得到∠BHN=∠EHB=90°,根据全等三角形的性质即可得到结论;
②由①知,BN=BE,根据线段的和差和等量代换即可得到结论.
解答 解:(1)∵BD=BC,
∴∠BDC=∠C,
∵AB=AC,
∴∠ABC=∠C,
∴∠A=∠DBC,
∵AD=BD,
∴∠A=∠DBA,
∴∠A=∠DBA=∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠C,
∵∠A+∠ABC+∠C=5∠A=180°,
∴∠A=36°,∠C=72°;
故答案为:36,72;
(2)①∵∠A=∠ABD=36°,
∠B=∠C=72°,
∴∠ABD=∠CBD=36°,
∵BH⊥EN,
∴∠BHN=∠EHB=90°,
在△BNH与△EBH中,$\left\{\begin{array}{l}{∠NBH=∠EBH}\\{BH=BH}\\{∠BHE=∠BHN}\end{array}\right.$,
∴△BNH≌△EBH,
∴BN=BE,
∴△BNE是等腰三角形;
②CD=AN+CE,
理由:由①知,BN=BE,
∵AB=AC,
∴AN=AB-BN=AC-BE,
∵CE=BE-BC,
∵CD=AC-AD=AC-BD=AC-BC,
∴CD=AN+CE.
点评 本题考查了等腰三角形的判定与性质,全等三角形的判定与性质,熟练掌握等腰三角形的判定与性质是解题的关键.


科目:初中数学 来源: 题型:填空题
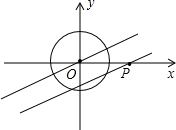 如图,⊙O是以坐标原点为圆心,半径为1的圆,过点O的直线l与x轴的正半轴所夹锐角为30°,点P在x轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.
如图,⊙O是以坐标原点为圆心,半径为1的圆,过点O的直线l与x轴的正半轴所夹锐角为30°,点P在x轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
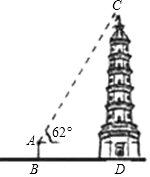 如图所示,位于昆明市昙华市内的瑞应塔,被誉为云南第一塔,某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度,甲同学在距离塔底部25m的B处地塔顶C的仰角为62°,若甲同学的眼睛到地面的高度AB为176cm,求瑞应塔C的高度(结果精确到0.1m,参考数据sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
如图所示,位于昆明市昙华市内的瑞应塔,被誉为云南第一塔,某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度,甲同学在距离塔底部25m的B处地塔顶C的仰角为62°,若甲同学的眼睛到地面的高度AB为176cm,求瑞应塔C的高度(结果精确到0.1m,参考数据sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
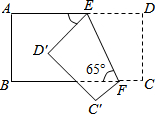 如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠C′FB等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠C′FB等于( )| A. | 70° | B. | 65° | C. | 50° | D. | 25° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com