
分析 (1)根据完全平方公式,可得答案;
(2)根据拆项法,可得互为相反数的项,根据分式的加减,可得答案.
解答 解:(1)原式=x2+3x+$\frac{9}{4}$=(x+$\frac{3}{2}$)2;
(2)原式=$\frac{1}{a-1}$+$\frac{1}{a-2}$-$\frac{1}{a-1}$+$\frac{1}{a-3}$-$\frac{1}{a-2}$+…+$\frac{1}{a-100}$-$\frac{1}{a-99}$
=$\frac{1}{a-100}$.
点评 本题考查了分式的加减,解(1)的关键是完全平方公式,解(2)的关键是拆项法得出互为相反数的项.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
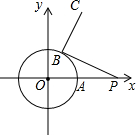 在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )| A. | 2$\sqrt{2}$π | B. | 4π | C. | 4$\sqrt{2}$π | D. | 6π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
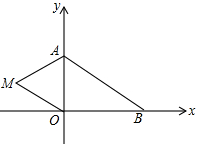 如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
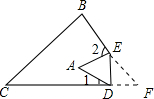 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2(∠1+∠2) | C. | 3∠A=2∠1+∠2 | D. | 2∠A=∠1+∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com