
分析 (1)先把方程化为一般式,找出a,b和c,求出根的判别式进行解答;
(2)先把x=-1代入原方程求出m的值,进而求出原方程的另一根.
解答 解:(1)∵(x+2)(x-m)=1,
∴x2+(2-m)x-2m-1=0,
∵a=1,b=2-m,c=-2m-1,
∴△=b2-4ac=4-4m+m2+8m+4=m2+4m+8=(m+2)2+4>0;
∴无论m取何实数,原方程总有两个不相等的实数根;
(2)∵原方程有一个根为-1,
∴-1-m=1,
∴m=-2,
∴x2+4x+3=0,
∴x1=-1,x2=-3,
∴方程的另一个根是x=-3.
点评 本题主要考查了根的判别式以及一元二次方程的解的知识,解答本题的关键是掌握根的判别式△>0?方程有两个不相等的实数根,此题难度不大.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
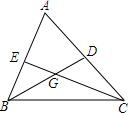 如图,在△ABC中,点G是△ABC的重心,BG和CG延长线分别交AC和AB于点D和E,则$\frac{GC}{CE}$的值为$\frac{2}{3}$.
如图,在△ABC中,点G是△ABC的重心,BG和CG延长线分别交AC和AB于点D和E,则$\frac{GC}{CE}$的值为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图题:如图,在△ABC所在的平面内找一点D,使D点到AB、AC两边的距离相等且到点A、点B的距离相等.(要求用尺规作图,保留作图痕迹)
作图题:如图,在△ABC所在的平面内找一点D,使D点到AB、AC两边的距离相等且到点A、点B的距离相等.(要求用尺规作图,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com