
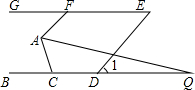
 如图,已知BC∥GE,AF∥DE,∠EDQ=50°.若AQ平分∠FAC,交BC于点Q,且∠Q=15°,则∠ACB的度数为80°.
如图,已知BC∥GE,AF∥DE,∠EDQ=50°.若AQ平分∠FAC,交BC于点Q,且∠Q=15°,则∠ACB的度数为80°. 分析 先根据BC∥EG得出∠E=∠1=50°,再由AF∥DE可知∠AFG=∠E=50°;再作AM∥BC,由平行线的传递性可知AM∥EG,故∠FAM=∠AFG,再根据AM∥BC可知∠QAM=∠Q,故∠FAQ=∠FAM+∠QAM,再根据AQ平分∠FAC可知∠MAC=∠QAC+∠QAM=80°,根据AM∥BC即可得出结论.
解答 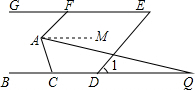 解:∵BC∥EG,
解:∵BC∥EG,
∴∠E=∠1=50°.
∵AF∥DE,
∴∠AFG=∠E=50°;
如图,作AM∥BC,
∵BC∥EG,
∴AM∥EG,
∴∠FAM=∠AFG=50°.
∵AM∥BC,
∴∠QAM=∠Q=15°,
∴∠FAQ=∠FAM+∠QAM=65°.
∵AQ平分∠FAC,
∴∠QAC=∠FA Q=65°,
∴∠M AC=∠QAC+∠QAM=80°.
∵AM∥BC,
∴∠ACB=∠MAC=80°.
故答案为:80°.
点评 本题考查的是平行线的性质,解题时注意:两直线平行,同位角相等;两直线平行,内错角相等.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形AOBC的两条边OA,OB的长是方程x2-18x+80=0的两根,其中OA<OB,沿直线AD将矩形折叠,使点C与y轴上的点E重合.
如图,矩形AOBC的两条边OA,OB的长是方程x2-18x+80=0的两根,其中OA<OB,沿直线AD将矩形折叠,使点C与y轴上的点E重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-1<k<$\frac{1}{4}$.
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-1<k<$\frac{1}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com