
如图所示,在平面上有过同一点P,并且半径相等的n个圆,其中任何两个圆都有两个交点,任何三个圆除P点外无其他公共点,那么试问:
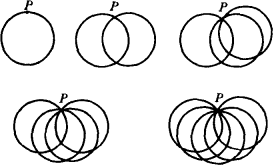
(1)这n个圆把平面划分成多少个平面区域?
(2)这n个圆共有多少个交点?
|
解析:(1)在图中,设以P点为公共点的圆有1,2,3,4,5个(取这n个特定的圆),观察平面被它们所分割成的平面区域有多少个?为此,我们列出下表.
由表易知 S2-S1=2,S3-S2=3,S3-S3=4,S5-S4=5,…… 由此,不难推测Sn-Sn-1=n. 把上面(n-1)个等式左、右两边分别相加,就得到 Sn-S1=2+3+4+…+n, 因为S1=2,所以 Sn=2+2+3+…+n=1+(1+2+3+…+n) 这就证明了当n个圆过点P时,可把平面划分为 下面对Sn-Sn-1=n,即Sn=Sn-1+n的正确性略作说明. 因为Sn-1为n-1个圆把平面划分的区域数,当再加上一个圆,即当n个圆过定点P时,这个加上去的圆必与前n-1个圆相交,所以这个圆就被前n-1个圆分成n部分,加在Sn-1上,所以有Sn=Sn-1+n. (2)与(1)一样,同样用观察、归纳、发现的方法来解决.为此,可列出下表. 由表容易发现
a1=1, a2-a1=1,a3-a2=2,a4-a3=3,a5-a4=4,…… an-1-an-2=n-2,an-an-1=n-1. n个式子相加 所以,当有满足条件的n个圆过P点时,这n个圆共有 |


科目:初中数学 来源: 题型:
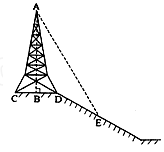
 9、如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为
9、如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第19-26期 总第175-182期 北师大版 题型:044
在如图所示的直角坐标平面上,表示下列各点:
(4,4),(1,4),(3,2),(8,2),(10,4),(4,4),(4,8),(8,7),(8,5),(4,6).
(1)用线段依次按照上述顺序把各点连接起来形成一个图案,这个图案像什么?
(2)把这些点的横坐标都加5,纵坐标不变,想象由这些点顺次连接形成的图案与(1)中的图案有什么关系?
(3)把题目中各点的横坐标不变,纵坐标都乘以-1,重新在图中描点、连线,得到的图案与(1)中的图案有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届四川新津县棕新中学八年级下学期期中考试数学卷(解析版) 题型:填空题
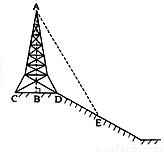
如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为 米。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com