
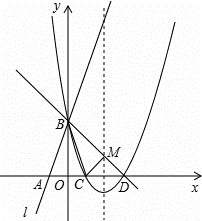
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
解:(1)直线BD的解析式为:y=-x+3.
抛物线的解析式为:y=x2﹣4x+3.
(2)抛物线的解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1).直线BD:y=﹣x+3与抛物线的对称轴交于点M,令x=2,得y=1,∴M(2,1).设对称轴与x轴交点为点F,则CF=FD=MN=1,
∴△MCD为等腰直角三角形.∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形.
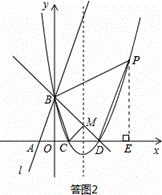 (I)若BD为斜边,则易知此时直角顶点为原点O,∴N1(0,0);
(I)若BD为斜边,则易知此时直角顶点为原点O,∴N1(0,0);
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,∴N2(﹣3,0);
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,∴N3(0,﹣3).
∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3).
(3)假设存在点P,使S△PBD=6,设点P坐标为(m,n).
(I)当点P位于直线BD上方时,如答图2所示:
过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3.
S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=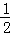 (3+n)•m﹣
(3+n)•m﹣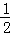 ×3×3﹣
×3×3﹣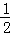 (m﹣3)•n=6,
(m﹣3)•n=6,
化简得:m+n=7 ①,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,代入①式整理得:m2﹣3m﹣4=0,
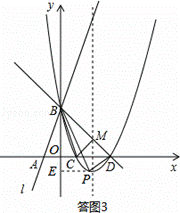 解得:m1=4,m2=﹣1,∴n1=3,n2=8,
解得:m1=4,m2=﹣1,∴n1=3,n2=8,
∴P1(4,3),P2(﹣1,8);
(II)当点P位于直线BD下方时,如答图3所示:
过点P作PE⊥y轴于点E,则PE=m,OE=﹣n,BE=3﹣n.
S△PBD=S梯形PEOD+S△BOD﹣S△PBE=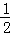 (3+m)•(﹣n)+
(3+m)•(﹣n)+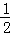 ×3×3﹣
×3×3﹣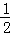 (3﹣n)•m=6,
(3﹣n)•m=6,
化简得:m+n=﹣1 ②,∵P(m,n)在抛物线上,∴n=m2﹣4m+3,
代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.
故此时点P不存在.
综上,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).


科目:初中数学 来源: 题型:
我市绿色和特色农产品在市场上颇具竞争力. 外贸商胡经理按市场价格10元/千克在我市收购了6000千克蘑菇存放入冷库中.请根据胡经理提供的预测信息(如右图)帮胡经理解决以下问题:
(1)若胡经理想将这批蘑菇存放x天后一次性出售,则x天后这批蘑菇的销售单价为 元,这批蘑菇的销售量是 千克;
(2)胡经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为100000元;(销售总金额=销售单价×销售量)
(3)将这批蘑菇存放多少天后一次性出售可获得最大
| |
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知在△ABC中,AB=8,BC=15,AC=17,则下列结论错误的是( ).
A.△ABC是直角三角形,且∠B=90°
B. △ABC是直角三角形,且∠A=60°
△ABC是直角三角形,且∠A=60°
C.△ABC是直 角三角形,且AC是它的斜边
角三角形,且AC是它的斜边
D.△ABC的面积为60
查看答案和解析>>
科目:初中数学 来源: 题型:
某校组织了一次向玉树地震灾区学校的捐款活动,其中初三(1)班50名学生捐款情况如下表所示,则捐款数据中5(元)的频数与频率分别是__________.
| 捐款(元) | 1 | 4 | 5 | 7 | 8 | 9 | 10 | 12 | 16 | 50 |
| 人数 | 1 | 3 | 6 | 5 | 5 | 3 | 15 | 7 | 4 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
把下列命题改写成“如果……那么……”的形式,并指出它是真命题还是假命题,如果是假命题,试举一反例说明.
(1)正方形的四个角都是直角;
(2)两角对应相等的两个三角形相似;
(3)不相交的两条直线互相平行.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com