
”¾ĢāÄæ”æijŠ£ĪŖĮĖ½āѧɜ¶Ō”°°²Č«³£Ź¶”±µÄÕĘĪÕ³Ģ¶Č£¬Ė껜³éČ”²æ·Öѧɜ°²Č«ÖŖŹ¶¾ŗČüµÄ²āŹŌ³É¼Ø×÷ĪŖŅ»øöŃł±¾£¬°“A£¬B£¬C£¬DĖÄøöµČ¼¶½ųŠŠĶ³¼Ę£¬ÖĘ³ÉĮĖČēĻĀ²»ĶźÕūµÄĶ³¼ĘĶ¼£®Ķ¼ÖŠA±ķŹ¾”°²»ĮĖ½ā”±£¬B±ķŹ¾”°ĮĖ½āŗÜÉŁ”±”¢C±ķŹ¾”°»ł±¾ĮĖ½ā”±£¬D±ķŹ¾”°·Ē³£ĮĖ½ā”±£®Ēėøł¾ŻĶ³¼ĘĶ¼ĖłĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
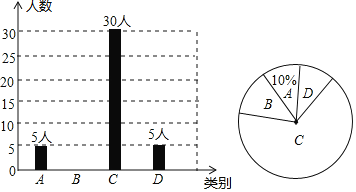
£Ø1£©±»µ÷²éµÄ×ÜČĖŹżŹĒ”” ””ČĖ£¬ÉČŠĪĶ³¼ĘĶ¼ÖŠA²æ·ÖĖł¶ŌÓ¦µÄÉČŠĪŌ²ŠÄ½ĒµÄ¶ČŹżĪŖ”” ””¶Č£»
£Ø2£©²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©ČōøĆŠ£¹²ÓŠŃ§Éś1500ČĖ£¬Ēėøł¾ŻÉĻŹöµ÷²é½į¹ū£¬¹Ą¼ĘøĆŠ£Ń§ÉśÖŠ“ļµ½”°»ł±¾ĮĖ½ā”±ŗĶ”°·Ē³£ĮĖ½ā”±¹²ÓŠ”” ””ČĖ£®
”¾“š°ø”æ£Ø1£©50£¬36£»£Ø2£©¼ū½āĪö£»£Ø3£©1050
”¾½āĪö”æ
£Ø1£©øł¾Ż”°A×éČĖŹż”ĀA×éµÄ°Ł·Ö±Č=×ÜČĖŹż”±£¬”°360”ć”ĮA×éµÄ°Ł·Ö±Č=A²æ·ÖĖł¶ŌÓ¦µÄÉČŠĪŌ²ŠÄ½ĒµÄ¶ČŹż”±£¬¼“æÉĒó½ā£»
£Ø2£©Ēó³öB×éČĖŹż£¬ŌŁ²¹Č«ĢõŠĪĶ³¼ĘĶ¼£¬¼“æÉ£»
£Ø3£©øł¾ŻŃ§Š£×ÜČĖŹż”ĮC”¢DĮ½×éČĖŹżµÄ°Ł·Ö±ČÖ®ŗĶ=øĆŠ£Ń§ÉśÖŠ“ļµ½”°»ł±¾ĮĖ½ā”±ŗĶ”°·Ē³£ĮĖ½ā”±µÄČĻŹ¶£¬¼“æÉĒó½ā£®
£Ø1£©5”Ā10%£½50£ØČĖ£©£¬360”ć”Į10%£½36”ć£¬
¹Ź“š°øĪŖ£ŗ50£¬36£»
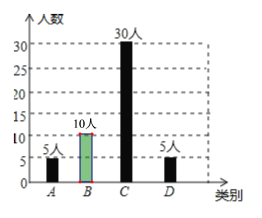
£Ø2£©50©5©30©5£½10£ØČĖ£©£¬²¹Č«ĢõŠĪĶ³¼ĘĶ¼ČēĶ¼ĖłŹ¾£ŗ
£Ø3£©1500”Į![]() £½1050£ØČĖ£©£¬
£½1050£ØČĖ£©£¬
¹Ź“š°øĪŖ£ŗ1050£®


 ±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷”¢Š”ĮĮ”¢Š”Ć·”¢Š”»ØĖÄČĖ¹²Ķ¬Ģ½¾æ“śŹżŹ½x2-4x+5µÄÖµµÄĒéæö£¬ĖūĆĒ×÷ĮĖČēĻĀ·Ö¹¤£ŗŠ”Ć÷øŗŌšÕŅÖµĪŖ1Ź±µÄxÖµ£¬Š”ĮĮøŗŌšÕŅÖµĪŖ0Ź±µÄxÖµ£¬Š”Ć·øŗŌšÕŅ×īŠ”Öµ£¬Š”»ØøŗŌšÕŅ×ī“óÖµ£®¼ø·ÖÖÓŗó£¬ø÷×ŌĶرØĢ½¾æµÄ½įĀŪ£¬ĘäÖŠ“ķĪóµÄŹĒ£Ø £©
A.Š”Ć÷ČĻĪŖÖ»ÓŠµ±x=2Ź±£¬x2-4x+5µÄÖµĪŖ1£»
B.Š”ĮĮČĻĪŖÕŅ²»µ½ŹµŹżx£¬Ź¹x2-4x+5µÄÖµĪŖ0£»
C.Š”»Ø·¢ĻÖµ±Č”“óÓŚ2µÄŹµŹżŹ±£¬x2-4x+5µÄÖµĖęxµÄŌö“ó¶ųŌö“ó£¬Ņņ“ĖČĻĪŖƻӊ×ī“óÖµ£»
D.Š”Ć··¢ĻÖx2-4x+5µÄÖµĖęxµÄ±ä»Æ¶ų±ä»Æ£¬Ņņ“ĖČĻĪŖƻӊ×īŠ”Öµ£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”÷ABC ÖŠ£¬AB£½AC£¬¹żĘäÖŠŅ»øö¶„µćµÄÖ±ĻßæÉŅŌ°ŃÕāøöČż½ĒŠĪ·Ö³ÉĮķĶāĮ½øöµČŃüČż½ĒŠĪ£¬Ōņ”ĻBAC£Ø £©
A. 36”ć£¬90”ć£¬![]() £¬ 108”ćB. 36”ć£¬72”ć£¬
£¬ 108”ćB. 36”ć£¬72”ć£¬![]() £¬90”ć
£¬90”ć
C. 90”ć£¬72”ć£¬108”ć£¬![]() D. 36”ć£¬90”ć£¬108”ć£¬
D. 36”ć£¬90”ć£¬108”ć£¬![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
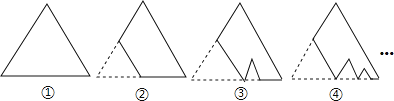
”¾ĢāÄæ”æČēĶ¼£¬Ķ¼¢ŁŹĒŅ»æé±ß³¤ĪŖ1£¬Öܳ¤¼ĒĪŖP1µÄµČ±ßČż½ĒŠĪÖ½°å£¬ŃŲĶ¼¢ŁµÄµ×±ß¼ōČ„Ņ»æé±ß³¤µÄ![]() µÄµČ±ßČż½ĒŠĪÖ½°åŗóµĆµ½Ķ¼¢Ś£¬Č»ŗóŃŲĶ¬Ņ»µ×±ßŅĄ“Ī¼ōČ„Ņ»æéøüŠ”µÄµČ±ßČż½ĒŠĪÖ½°å£Ø¼“Ęä±ß³¤ĪŖĒ°Ņ»æé±»¼ōµōµČ±ßČż½ĒŠĪÖ½°å±ß³¤µÄ
µÄµČ±ßČż½ĒŠĪÖ½°åŗóµĆµ½Ķ¼¢Ś£¬Č»ŗóŃŲĶ¬Ņ»µ×±ßŅĄ“Ī¼ōČ„Ņ»æéøüŠ”µÄµČ±ßČż½ĒŠĪÖ½°å£Ø¼“Ęä±ß³¤ĪŖĒ°Ņ»æé±»¼ōµōµČ±ßČż½ĒŠĪÖ½°å±ß³¤µÄ![]() £©ŗ󣬵ĆĶ¼¢Ū£¬¢Ü£¬”£¬¼ĒµŚn£Øn”Ż3£©æéÖ½°åµÄÖܳ¤ĪŖPn£¬ŌņPn-Pn-1=_________
£©ŗ󣬵ĆĶ¼¢Ū£¬¢Ü£¬”£¬¼ĒµŚn£Øn”Ż3£©æéÖ½°åµÄÖܳ¤ĪŖPn£¬ŌņPn-Pn-1=_________
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øłÖńøĶ³¤![]() Ć×£¬ĻČĻń
Ć×£¬ĻČĻń![]() ææĒ½·ÅÖĆ£¬ÓėĖ®Ę½¼Š½ĒĪŖ
ææĒ½·ÅÖĆ£¬ÓėĖ®Ę½¼Š½ĒĪŖ![]() £¬ĪŖĮĖ¼õÉŁÕ¼µŲæռ䣬ĻÖ½«ÖńøĶĻń
£¬ĪŖĮĖ¼õÉŁÕ¼µŲæռ䣬ĻÖ½«ÖńøĶĻń![]() ·ÅÖĆ£¬ÓėĖ®Ę½¼Š½ĒĪŖ
·ÅÖĆ£¬ÓėĖ®Ę½¼Š½ĒĪŖ![]() £¬ŌņÖńøĶČĆ³ö¶ąÉŁĖ®Ę½æÕ¼ä£Ø £©
£¬ŌņÖńøĶČĆ³ö¶ąÉŁĖ®Ę½æÕ¼ä£Ø £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖ·Ö±š“ÓA£¬BĮ½µŲĶ¬Ź±³ö·¢£¬ŌČĖŁĻąĻņ¶ųŠŠ£®¼×µÄĖŁ¶Č“óÓŚŅŅµÄĖŁ¶Č£¬¼×µ½“ļBµŲŗó£¬ŅŅ¼ĢŠųĒ°ŠŠ£®Éč³ö·¢xhŗó£¬Į½ČĖĻą¾ąykm£¬Ķ¼ÖŠÕŪĻß±ķŹ¾“ÓĮ½ČĖ³ö·¢ÖĮŅŅµ½“ļAµŲµÄ¹ż³ĢÖŠyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£®
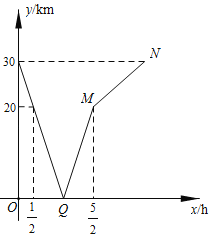
£Ø1£©øł¾ŻĶ¼ÖŠŠÅĻ¢£¬Ēó³öµćQµÄ×ų±ź£¬²¢ĖµĆ÷ĖüµÄŹµ¼ŹŅāŅ壻
£Ø2£©Ēó¼×”¢ŅŅĮ½ČĖµÄĖŁ¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£¬²¢°“ŅŖĒó½ā“š£®
£ØÄ£ŠĶ½ØĮ¢£©ČēĶ¼¢Ł£¬µČŃüÖ±½ĒČż½ĒŠĪABCÖŠ£¬”ĻACB£½90”ć£¬CB£½CA£¬Ö±ĻßED¾¹żµćC£¬¹żA×÷AD”ĶEDÓŚµćD£¬¹żB×÷BE”ĶEDÓŚµćE£®ĒóÖ¤£ŗ”÷BEC”Õ”÷CDA£®
£ØÄ£ŠĶÓ¦ÓĆ£©
Ó¦ÓĆ1£ŗČēĶ¼¢Ś£¬ŌŚĖıߊĪABCDÖŠ£¬”ĻADC£½90”ć£¬AD£½6£¬CD£½8£¬BC£½10£¬AB2£½200£®ĒóĻ߶ĪBDµÄ³¤£®
Ó¦ÓĆ2£ŗČēĶ¼ ¢Ū£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö½Ę¬”÷OPQĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬QO£½QP£¬P£Ø4£¬m£©£¬µćQŹ¼ÖÕŌŚÖ±ĻßOPµÄÉĻ·½£®
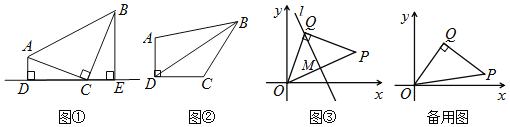
£Ø1£©ÕŪµžÖ½Ę¬£¬Ź¹µĆµćPÓėµćOÖŲŗĻ£¬ÕŪŗŪĖłŌŚµÄÖ±Ļßl¹żµćQĒŅÓėĻ߶ĪOP½»ÓŚµćM£¬µ±m£½2Ź±£¬ĒóQµćµÄ×ų±źŗĶÖ±ĻßlÓėxÖįµÄ½»µć×ų±ź£»
£Ø2£©ČōĪŽĀŪmČ”ŗĪÖµ£¬µćQ×ÜŌŚÄ³ĢõČ·¶ØµÄÖ±ĻßÉĻ£¬ĒėÖ±½ÓŠ“³öÕāĢõÖ±ĻߵĽāĪöŹ½”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
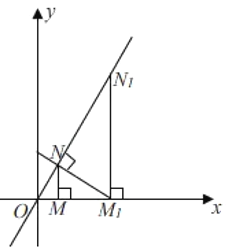
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÖ±Ļß![]() ¾¹żŌµć
¾¹żŌµć![]() £¬
£¬![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÖįµÄ“¹Ļß½»Ö±Ļß
ÖįµÄ“¹Ļß½»Ö±Ļß![]() ÓŚµć
ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷Ö±Ļß
×÷Ö±Ļß![]() µÄ“¹Ļß½»
µÄ“¹Ļß½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £»¹żµć
£»¹żµć![]() ×÷
×÷![]() ÖįµÄ“¹Ļß½»Ö±Ļß
ÖįµÄ“¹Ļß½»Ö±Ļß![]() ÓŚµć
ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷Ö±Ļß
×÷Ö±Ļß![]() µÄ“¹Ļß½»
µÄ“¹Ļß½»![]() ÖįÓŚµć
ÖįÓŚµć![]() °““Ė×÷·Ø¼ĢŠųĻĀČ„£¬Ōņµć
°““Ė×÷·Ø¼ĢŠųĻĀČ„£¬Ōņµć![]() µÄ×ų±źĪŖ__________.
µÄ×ų±źĪŖ__________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ![]() ĪŖŌµć£¬µć
ĪŖŌµć£¬µć![]() ¼°ŌŚµŚŅ»ĻóĻŽµÄ¶Æµć
¼°ŌŚµŚŅ»ĻóĻŽµÄ¶Æµć![]() £¬ĒŅ
£¬ĒŅ![]() £¬Éč
£¬Éč![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() .
.
£Ø1£©Ēó![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄŗÆŹż½āĪöŹ½£»
µÄŗÆŹż½āĪöŹ½£»
£Ø2£©Ēó![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø3£©µ±![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µć×ų±ź£»
µć×ų±ź£»
£Ø4£©»³öŗÆŹż![]() µÄĶ¼Ļó.
µÄĶ¼Ļó.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com