
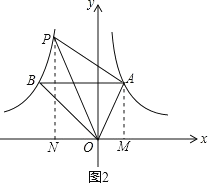
【题目】如图,点A是反比例函数![]() (x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数
(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数![]() (k<0,x<0)的图象于点B,且S△AOB=5.
(k<0,x<0)的图象于点B,且S△AOB=5.
(1) k的值为_______;
(2) 若点A的横坐标是1,
①求∠AOB的度数;
②在y2的图象上找一点P(异于点B), 使S△AOP=S△AOB,求点P的坐标.

【答案】-8
【解析】试题分析:(1)首先设AB交y轴于点C,由点A是反比例函数![]() (x>0)图象上的任意一点,AB∥x轴,根据反比例函数系数
(x>0)图象上的任意一点,AB∥x轴,根据反比例函数系数![]() 的几何意义求得
的几何意义求得![]() 的面积,又由
的面积,又由![]() 的面积等于5,可求得
的面积等于5,可求得![]() 的面积,继而求得
的面积,继而求得![]() 的值;
的值;
(2)①由点A的横坐标是1,可求得点A的坐标,继而求得点![]() 的纵坐标,则可求得点
的纵坐标,则可求得点![]() 的坐标,则可求得
的坐标,则可求得![]() 的长,然后由勾股定理的逆定理,求得
的长,然后由勾股定理的逆定理,求得![]() 的度数;
的度数;
②过点A作AM⊥x轴于点A,过点P作PN⊥x轴于点N,设![]() 根据反比例函数系数k的几何意义得出
根据反比例函数系数k的几何意义得出![]() 由S△AOP=S△梯形APNMS△NOPS△AOM=S△AOB=5,列出方程
由S△AOP=S△梯形APNMS△NOPS△AOM=S△AOB=5,列出方程![]()
解方程即可.
试题解析:(1)如图1,设AB交y轴于点C,
∵点A是反比例函数![]() (x>0)图象上的任意一点,且AB∥x轴,
(x>0)图象上的任意一点,且AB∥x轴,
∴AB⊥y轴,
![]()
![]()
∴![]()
∵反比例函数![]() (k<0,x<0)的图象过点B,AB⊥y轴,
(k<0,x<0)的图象过点B,AB⊥y轴,
![]()
∴k=8;
故答案为:8;
(2)①∵点A的横坐标是1,
![]()
∴点A(1,2),
∵AB∥x轴,
∴点B的纵坐标为2,
![]()
解得:x=4,
∴点B(4,2),
![]() ∴
∴![]()
![]()
②如图2,过点A作AM⊥x轴于点A,过点P作PN⊥x轴于点N,设![]()
则![]()
∵S△AOP=S△梯形APNMS△NOPS△AOM=S△AOB=5,
![]()
整理,得![]()
解得![]() (不合题意舍去),
(不合题意舍去),
∴点P的坐标为(1,8).


科目:初中数学 来源: 题型:
【题目】计算:
(1)8+(-![]() )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|-![]() |÷(
|÷(![]() -
-![]() )×(-4)2.
)×(-4)2.
(3)(![]() -
-![]() +
+![]() )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-![]() )÷3×[2-(-3)2].
)÷3×[2-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在精准扶贫中,李师傅在当地政府的扶持下,去年下半年,他开办的桌椅加工厂取得了非常好的经济效益,他决定制作一批课桌捐赠给山区学校:已知制作一张桌子要用一个桌面和4条桌腿,1m3木材可制作20个桌面,或者制作400条桌腿,现有12m3木材,应怎样计划用料才能制作尽可能多的桌子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个一元一次方程的一次项系数与常数项的差刚好是这个方程的解,则称这个方程为妙解方程.例如:方程![]() 中,
中,![]() ,方程的解为
,方程的解为![]() ,则方程
,则方程![]() 为妙解方程.请根据上述定义解答下列问题:
为妙解方程.请根据上述定义解答下列问题:
(1)方程![]() 是妙解方程吗?试说明理由.
是妙解方程吗?试说明理由.
(2)已知关于![]() 的一元一次方程
的一元一次方程![]() 是妙解方程.求
是妙解方程.求![]() 的值.
的值.
(3)已知关于![]() 的一元一次方程
的一元一次方程![]() 是妙解方程,并且它的解是
是妙解方程,并且它的解是![]() .求代数式
.求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上标出的所有点中,任意相邻两点间的距离相等,已知点A表示﹣12,点G表示6.
![]()
(1)表示原点的点是 ,点C表示的数是 ;
(2)数轴上有两点M、N,点M到点D的距离为![]() ,点N到点D的距离为4,求点M,N之间的距离;
,点N到点D的距离为4,求点M,N之间的距离;
(3)点P为数轴上一点,且表示的数是整数,点P到点A的距离与点P到点G的距离之和为18,则这样的点P有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
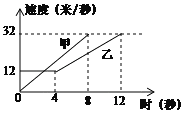
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
查看答案和解析>>
科目:初中数学 来源: 题型:
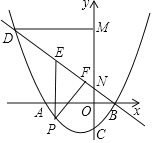
【题目】如图,抛物线![]() 与x轴交于A、B两点,其中点
与x轴交于A、B两点,其中点![]() ,交y轴于点
,交y轴于点![]() 直线
直线![]() 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点
过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点![]() 不与点B、D重合
不与点B、D重合![]() ,过点P作y轴的平行线,交直线BD于点E,过点D作
,过点P作y轴的平行线,交直线BD于点E,过点D作![]() 轴于点M.
轴于点M.
![]() 求抛物线
求抛物线![]() 的表达式及点D的坐标;
的表达式及点D的坐标;
![]() 若四边形PEMN是平行四边形?请求出点P的坐标;
若四边形PEMN是平行四边形?请求出点P的坐标;
![]() 过点P作
过点P作![]() 于点F,设
于点F,设![]() 的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com