
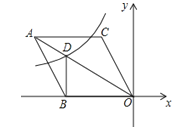
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
【答案】D
【解析】首先过点C 作CE⊥x 轴于点E,由∠BOC=60°,顶点C 的坐标为(m ,3![]() ),可求 得OC 的长,又由菱形ABOC 的顶点O 在坐标原点,边BO 在x 轴的负半轴上,可求 得OB 的长,且∠AOB=30°,继而求得DB 的长,则可求得点D 的坐标,又由反比例 函数
),可求 得OC 的长,又由菱形ABOC 的顶点O 在坐标原点,边BO 在x 轴的负半轴上,可求 得OB 的长,且∠AOB=30°,继而求得DB 的长,则可求得点D 的坐标,又由反比例 函数![]() 的图象与菱形对角线AO 交D 点,即可求得答案.
的图象与菱形对角线AO 交D 点,即可求得答案.
解:过点C 作CE⊥x 轴于点E,
∵顶点C 的坐标为(m ,3![]() ),
),
∴OE= ﹣m ,CE=3![]() ,
,
∵菱形ABOC 中,∠BOC=60°,
∴OB=OC=![]() =6 ,∠BOD=
=6 ,∠BOD=![]() ∠BOC=30°,
∠BOC=30°,
∵DB⊥x 轴,
∴DB=OBtan30°=6×![]() =2
=2![]() ,
,
∴点D 的坐标为:(﹣6,2![]() ),
),
∵反比例函数![]() 的图象与菱形对角线AO 交D 点,
的图象与菱形对角线AO 交D 点,
∴k=xy= ﹣12![]() .
.
故选D.
“点睛”此题考查了菱形的性质以及反比例函数图象上点的坐标特征.注意准确作出辅助线,
求得点D 的坐标是关键.


科目:初中数学 来源: 题型:
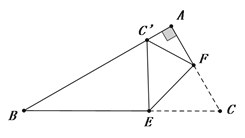
【题目】如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC=![]() +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为_____________.
+1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点![]() ,其中
,其中![]() ,
,![]() ,如图所示,设点
,如图所示,设点![]() 所对应数的和是
所对应数的和是![]() .
.
(1)若以![]() 为原点,则点
为原点,则点![]() 所对应的数是____,点
所对应的数是____,点![]() 所对应的数是_____,
所对应的数是_____,![]() ______.
______.
(2)若原点![]() 在图中数轴上点
在图中数轴上点![]() 的右边,且
的右边,且![]() ,求
,求![]() .
.
(3)若![]() , 求点
, 求点![]() 分别对应的数.
分别对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法计算:
(1)0.36+(-7.4)+0.5+(-0.6)+0.14;
(2)(-2.125)+![]() +(-3.2);
+(-3.2);
(3)![]() .
.
(4)|-0.75|+(-3)-(-0.25)+![]() .
.
(5)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解答下列问题:

(1)义乌市为了搞好“五水共治”工作,将一段长为![]() 的河道任务交由甲乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治
的河道任务交由甲乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治![]() ,乙工程队每天整治
,乙工程队每天整治![]() ,试求甲乙两个工程队分别整治了多长的河道.
,试求甲乙两个工程队分别整治了多长的河道.
(2)小玲在数学书上发现如图所示的题目,两个方框表示的是同一个数,请你帮小玲求出方框所表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
①8+(﹣10)+(﹣2)﹣(﹣5)
②2![]() ﹣3
﹣3![]() ﹣5
﹣5![]() ﹣|﹣3
﹣|﹣3![]() |
|
③(﹣1![]() )+1.25+(﹣8.5)+10
)+1.25+(﹣8.5)+10![]()
④(![]() )×(﹣12)
)×(﹣12)
⑤(﹣199![]() )×5(用简便方法计算)
)×5(用简便方法计算)
⑥10×(﹣![]() )﹣2×
)﹣2×![]() +(﹣3)×(﹣
+(﹣3)×(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4.若用想x,y表示直角三角形的两直角边(x>y),则下列四个说法:①![]() ,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )
,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )

A. ①②B. ①②③④C. ②④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在方程ax=12(a是正整数)中,x是未知数,a是用字母表示的已知数。于是,在项ax中,字母a是_____________,我们把a叫做_____________。这个方程是含有系数的_____________。在方程![]() 中,
中,![]() 是未知数,b和s是用字母表示的已知数。同样地,字母b是______________字母s也叫做__________________,这个方程是含有系数的_____________。
是未知数,b和s是用字母表示的已知数。同样地,字母b是______________字母s也叫做__________________,这个方程是含有系数的_____________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com