
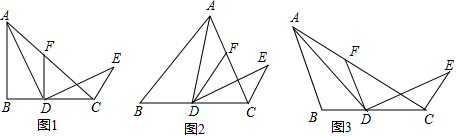
���� ��1����ͼ1�У���AC��DE���ڵ�O��ֻҪ֤����ADF=��EDC��DF=DC����֤����ADF�ա�EDC�������á�8���͡�֤����ACE=��ADE��
��2��A����DE��AC���ڵ�O��ֻҪ֤����ADF�ա�EDC�������á�8���͡�֤����ACE=��ADE��
B���ٲ��룺��ACE=����֤����������A���ڽ��۲��䣮֤���������Ƣ٣�
��� �⣺��1����ͼ1�У���AC��DE���ڵ�O��
��BA=BC����B=90�㣬
���BAC=��ACB=45�㣬
��DF��AB��
���FDC=��B=90��=��ADE����DFC=��BAC=45�㣬
���ADF=��EDC����DFC=��DCF��
��DF=DC��
�ڡ�ADF�͡�EDC�У�
$\left\{\begin{array}{l}{DA=DE}\\{��ADF=��EDC}\\{DF=DC}\end{array}\right.$��
���ADF�ա�EDC��
���DAO=��E��
�ߡ�AOD=��EOC��
���ACE=��ADO=90�㣬
�ʴ�Ϊ��EDC��90�㣮
��2��ѡA��B��
�ʴ�ΪA��B��
A����ͼ2�У���DE��AC���ڵ�O��
��DF��AB��
���FDC=��B=��ADE����DFC=��BAC��
���ADF=��EDC��
��BA=BC��
���BAC=��BCA��
���DCF=��DFC��
��DF=DC��
�ڡ�ADF�͡�EDC�У�
$\left\{\begin{array}{l}{DA=DE}\\{��ADF=��EDC}\\{DF=DC}\end{array}\right.$��
���ADF�ա�EDC��
���DAO=��E��
�ߡ�AOD=��EOC��
���ACE=��ADO=50�㣮
B�����룺��ACE=�����������£�
��ͼ3�У���DE��AC���ڵ�O��
��DF��AB��
���FDC=��B=��ADE����DFC=��BAC��
���ADF=��EDC��
��BA=BC��
���BAC=��BCA��
���DCF=��DFC��
��DF=DC��
�ڡ�ADF�͡�EDC�У�
$\left\{\begin{array}{l}{DA=DE}\\{��ADF=��EDC}\\{DF=DC}\end{array}\right.$��
���ADF�ա�EDC��
���DAO=��E��
�ߡ�AOD=��EOC��
���ACE=��ADO=����
��ͼ4�У���D���߶�CB���ӳ�����ʱ����ACE=��ADE=�������۲��䣮֤���������Ƣ٣�
���� ���⿼���������ۺ��⡢���������ε����ʡ�ȫ�������ε��ж������ʡ�����ֱ�������ε��ж������ʵ�֪ʶ������Ĺؼ�����ȷѰ��ȫ�������ν�����⣬ѧ�����á�8���͡�֤������ȣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
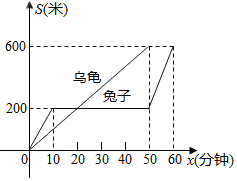 ���������ܡ���ͬѧ����Ϥ��Ԣ�Թ��£�ͼ�б�ʾ·��S���ף���ʱ��t���֣�֮��Ĺ�ϵ����ô����֪����
���������ܡ���ͬѧ����Ϥ��Ԣ�Թ��£�ͼ�б�ʾ·��S���ף���ʱ��t���֣�֮��Ĺ�ϵ����ô����֪�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=-x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����A������Ϊ��-1��0������y�ύ�ڵ�C��0��3������ֱ��BC������P��x�����˶�������P��PM��x�ᣬ���������ڵ�M����ֱ��BC�ڵ�N�����P�ĺ�����Ϊm��
��ͼ��������y=-x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����A������Ϊ��-1��0������y�ύ�ڵ�C��0��3������ֱ��BC������P��x�����˶�������P��PM��x�ᣬ���������ڵ�M����ֱ��BC�ڵ�N�����P�ĺ�����Ϊm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
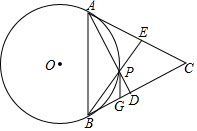 ��ͼ����P�ǵȱ�������ABC�ڲ�һ�����㣬��APB=120�㣬��O�ǡ�APB�����Բ��AP��BP���ӳ��߷ֱ�BC��AC��D��E��
��ͼ����P�ǵȱ�������ABC�ڲ�һ�����㣬��APB=120�㣬��O�ǡ�APB�����Բ��AP��BP���ӳ��߷ֱ�BC��AC��D��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x+7}{3}$=$\frac{x}{4}$+1 | B�� | $\frac{x+7}{3}$=$\frac{x}{4}$-1 | C�� | $\frac{x-7}{3}$=$\frac{x}{4}$+1 | D�� | $\frac{x-7}{3}$=$\frac{x}{4}$-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com