练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在直线l上取一点A，顺次截取AB=BC=a，CD=b，

    那么

    AC=AB＋(　　)=a＋(　　)=(　　)，

    AC=(　　)－CD=(　　)－b=(　　)，

    BC=AD－(　　)－(　　)=(　　)－(　　)－(　　)=(　　)．

    答案：略
    解析：

    解　AC=AB＋(BC)=a＋(a)=2a，

    AC=(AD)－CD=(a＋a＋b)－b=2a，

    BC=AD－(AB)－(CD)=(a＋a＋b)－a－b=a．


    提示：

    线段的和差与它们长度的和差是一致的．由图上可直观地看到．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    24、如图，为了确定一条经过点D且与直线AB平行的直线，小明同学在直线AB上取一点C，在直线AB外取一点E，恰好量得∠2=80°，∠D=50°，∠1=∠3，这时，小明说AB与DE平行了，他说得对吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面坐标系中有一正三角形ABC，A（-8，0）、B（8，0），直线l经过原点O及BC的中点D，另一动直线a平行于y轴，从原点出发，以每秒1个单位长度的速度沿x轴向右平移，直线a分别交线段BC、直线l于点E、F，以EF为边向左侧作等边△EFG，设△EFG与△ABC重叠部分的面积为S（平方单位），当点G落在y轴上时，a停止运动，设直线a的运动时间为t（秒）．
    （1）直接写出：C点坐标
     
    ，直线l的解析式：
     
    ．
    （2）请用含t的代数式表示线段EF；
    （3）求出S关于t的函数关系式及t的取值范围．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•顺义区二模）问题：如果存在一组平行线a∥b∥c，请你猜想是否可以作等边三角形ABC使其三个顶点分别在a、b、c上？
    小明同学的解答如下：如图1所示，过点A作AM⊥b于M，作∠MAN=60°，且AN=AM，过点N作CN⊥AN交直线c于点C，在直线b上取点B使BM=CN，则△ABC为所求．

    （1）请你参考小明的作法，在图2中作一个等腰直角三角形DEF使其三个顶点分别在a、b、c上，点D为直角顶点；
    （2）若直线a、b之间的距离为1，b、c之间的距离为2，则在图2中，S△DEF=
    5
    5
    ，在图1中AC=
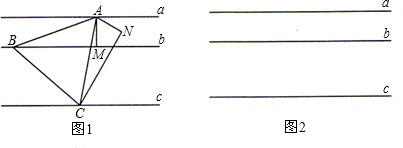
    2
    3
    		21
    2
    3
    		21
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

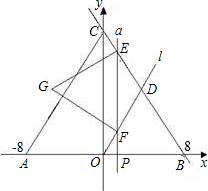
    已知直线l：y=－x+m（m≠0）交x轴、y轴于A、B两点，点C、M分别在

    线段OA、AB上，且OC=2CA，AM=2MB，连接MC，将△ACM绕点M

    旋转180°，得到△FEM，则点E在y轴上, 点F在直线l上;取线段EO中

    点N,将ACM沿MN所在直线翻折，得到△PMG，其中P与A为对称点.记：

    过点F的双曲线为6ec8aac122bd4f6e，过点M且以B为顶点的抛物线为6ec8aac122bd4f6e，过点P且以M

    为顶点的抛物线为6ec8aac122bd4f6e.(1) 如图，当m=6时，①直接写出点M、F的坐标，

    ②求6ec8aac122bd4f6e、6ec8aac122bd4f6e的函数解析式；

    （2）当m发生变化时， ①在6ec8aac122bd4f6e的每一支上，y随x的增大如何变化？请说明理由。

                          ②若6ec8aac122bd4f6e、6ec8aac122bd4f6e中的y都随着x的增大而减小,写出x的取值范围。

    6ec8aac122bd4f6e
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：

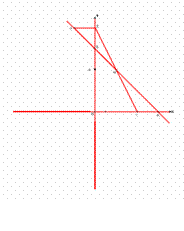
    已知直线l：y=－x+m（m≠0）交x轴、y轴于A、B两点，点C、M分别在

    线段OA、AB上，且OC=2CA，AM=2MB，连接MC，将△ACM绕点M

    旋转180°，得到△FEM，则点E在y轴上, 点F在直线l上;取线段EO中

    点N,将ACM沿MN所在直线翻折，得到△PMG，其中P与A为对称点.记：

    过点F的双曲线为，过点M且以B为顶点的抛物线为，过点P且以M

    为顶点的抛物线为.

    (1) 如图10，当m=6时，①直接写出点M、F的坐标，

    ②求、的函数解析式；

    （2）当m发生变化时， ①在的每一支上，y随x的增大如何变化？请说明理由。

                          ②若、中的y都随着x的增大而减小,写出x的取值范围。

    查看答案和解析>>

    同步练习册答案