


分析 (1)过点作BH∥EG交CD于点H,由ASA定理得出△ABF≌△BCH,根据全等三角形的性质证明结论;
(2)作BM∥GE交CD于点M,作AN∥HF交BC于点N,根据直角三角形的性质和四边形ABCD是矩形,由相似三角形的性质得出△ABN∽△BCM,根据相似三角形的对应边成比例即可得出结论;
(3)根据勾股定理得到(4-a)2+(3+b)2=52,根据a=b解方程即可;
(4)过点B作DC的平行线,过点C作OF的平行线,两线交于点P,连接AP,由题意可得DBPC为平行四边形,故可得出∠BAP=∠3+∠1=∠BPA=∠4+∠2.若a<b,即AC<BD=CP,因而在△ACP中,由等边对等角可知∠3<∠5,再由锐角三角函数的定义即可得出结论.
解答 解:(1)作BH∥EG交CD于点H.则BH=EG.
∵AF⊥EG,
∴BH⊥AF,
∴∠BIF=90°,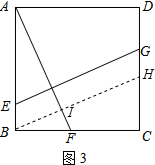
∴∠IBF+∠AFB=90°,
又∵直角△ABF中,∠BAF+∠AFB=90°,
∴∠BAF=∠IBF,
∴在△ABF和△BCH中,
$\left\{\begin{array}{l}{∠BAF=∠IBF}\\{AB=BC}\\{∠ABF=∠C}\end{array}\right.$,
∴△ABF≌△BCH,
∴AF=BH,
∴AF=EG;
(2)同理作BM∥EG交CD于点M,作AN∥HF交BC于点N.
同(1)可得∠BAN=∠MBC,
又∵∠ABN=∠C,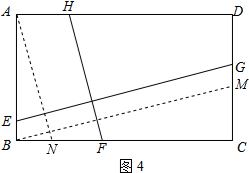
∴△ABN∽△BCM,
∴$\frac{AN}{BM}=\frac{AB}{BC}$=$\frac{2}{x}$,
又HF=AN,EG=BM,
∴y=$\frac{2}{x}$;
(3)解:∵CO=4-a,DO=3+b.
∴Rt△DOC中,DC2=(4-a)2+(3+b)2,
即(4-a)2+(3+b)2=52.
当a=b时,有(4-a)2+(3+a)2=25,
解得a=1或a=0(不合).
故答案为:1;
(4)当0<a<1时,a<b.理由如下:
如图5,过点B作DC的平行线,过点C作OF的平行线,两线交于点P,连接AP.
∵CD∥BP,PC∥OF,
∴DBPC为平行四边形,
∴BP=DC,CP=BD.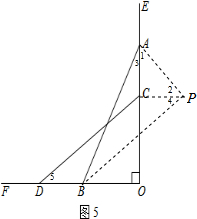
又AB=DC,
∴BP=AB.
∴∠BAP=∠3+∠1=∠BPA=∠4+∠2.
若a<b,即AC<BD=CP,因而在△ACP中,
∵∠1>∠2,
∴∠3<∠4.
又∵∠5=∠4,
∴∠3<∠5.
∵Rt△ABO中,sin∠3=$\frac{OB}{AB}$=$\frac{3}{5}$,
同理sin∠5=$\frac{OC}{CD}$=$\frac{4-a}{5}$,
∴$\frac{4-a}{5}$>$\frac{3}{5}$,
解得,0<a<1.
点评 本题考查的是四边形综合题,掌握平行四边形的判定与性质、全等三角形的判定与性质、勾股定理的应用以及一元二次方程的解法是解题的关键,解答时注意锐角三角函数的定义的应用.


科目:初中数学 来源: 题型:选择题
| A. | 2.16 | B. | 2.15 | C. | 2.14 | D. | 2.13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>0 | B. | m>1 | C. | m<0 | D. | m<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x≥$\frac{1}{3}$ | D. | x≥-$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )| A. | 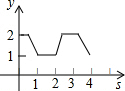 | B. | 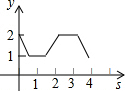 | C. | 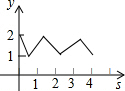 | D. | 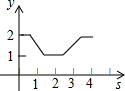 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
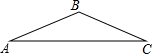 如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )
如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )| A. | 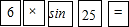 | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
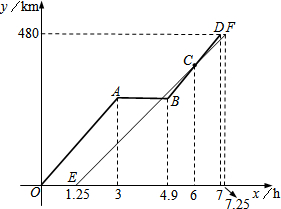 “十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.
“十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
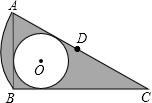 如图,在Rt△ABC中,AB=1,∠ACB=30°,点D是AC的中点,⊙O是△ABC的内切圆,以点D为圆心,以AD的长为半径作$\widehat{AB}$,则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,AB=1,∠ACB=30°,点D是AC的中点,⊙O是△ABC的内切圆,以点D为圆心,以AD的长为半径作$\widehat{AB}$,则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com