
 如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区.
如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区.分析 (1)先证明∠CAB=∠ACB,可得CB=AB,再根据路程=速度×时间就是健康求解;
(2)过点C作CE⊥AD,垂足为点E,根据锐角三角函数的概念求出CE,与50海里比较即可.
解答 解:(1)由题意得∠CBD=60°,∠CAB=30°,
∴∠ACB=30°,
∴∠CAB=∠ACB,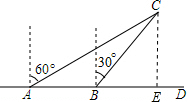 ∴CB=AB=40×1.5=60(海里),
∴CB=AB=40×1.5=60(海里),
∴B处到小岛C的距离为60海里;
(2)过点C作CE⊥AD,垂足为点E,
∵CE=CB×sin∠CBE=60×sin60°=30$\sqrt{3}$≈51.96海里,
∴CE>50,
∴轮船从B处继续向正东方向航行,没有触礁危险.
点评 本题考查的是解直角三角形的应用-方向角问题,正确根据题意画出图形、准确标注方向角、熟练掌握锐角三角函数的概念是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
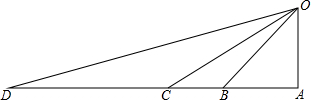 政府为开发“江心岛O”,从仓储D处调集物资,计划先用汽车运到与D在同一直线上的C,B,A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,
政府为开发“江心岛O”,从仓储D处调集物资,计划先用汽车运到与D在同一直线上的C,B,A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+1>y+1 | B. | x2>y2 | C. | $\frac{x}{2}>\frac{y}{2}$ | D. | 2x>2y |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com