
 已知:一次越野赛中,当小明跑了1600米时,小强跑了1400米.小明,小强此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示.
已知:一次越野赛中,当小明跑了1600米时,小强跑了1400米.小明,小强此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示.分析 (1)根据函数图象可以看出谁先到达终点;
(2)根据函数图象可以列出相应的二元一次方程组,从而可以解答本题.
解答 解:(1)由图象可知,小强先到达终点;
(2)设小明从1600处到终点的速度为a米/秒,小强从1400米处到终点的速度为b米/秒,
$\left\{\begin{array}{l}{1600+300a=1400+200b}\\{200a=100b}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=2}\\{b=4}\end{array}\right.$,
故这次越野跑的全程为:1600+300×2=1600+600=2200(米),
即这次越野跑的全程为2200米.
点评 本题考查一次函数的应用、二元一次方程组的应用,解题的关键是明确题意,列出相应的方程组,利用数形结合的思想解答问题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
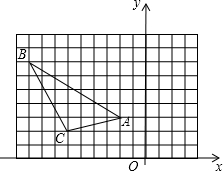 如图,在直角坐标系中,△ABC的顶点都在网格点上(方格纸中每个小正方形边长为1),将△ABC向右平移4格,再向下平移2格.
如图,在直角坐标系中,△ABC的顶点都在网格点上(方格纸中每个小正方形边长为1),将△ABC向右平移4格,再向下平移2格.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
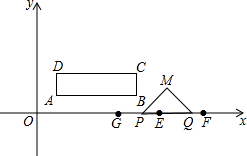 如图,矩形的四个顶点为A(1,1)、B(5,1)、C(5,2)、D(1,2),点E、F的坐标分别为(6,0)、(8,0),动点P从点E出发,以每秒2个单位长度的速度沿EO匀速运动,到达点O后立即以原来的速度沿OE返回;另一动点Q从点F出发,以每秒1个单位长度的速度沿FO匀速运动,点P、Q同时出发,两点相遇时停止运动,在点P、Q的运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQM.设运动时间为t.
如图,矩形的四个顶点为A(1,1)、B(5,1)、C(5,2)、D(1,2),点E、F的坐标分别为(6,0)、(8,0),动点P从点E出发,以每秒2个单位长度的速度沿EO匀速运动,到达点O后立即以原来的速度沿OE返回;另一动点Q从点F出发,以每秒1个单位长度的速度沿FO匀速运动,点P、Q同时出发,两点相遇时停止运动,在点P、Q的运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQM.设运动时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0),下列说法:
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0),下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com