Question

已知直线y=（m-1）x+3与函数y=x²+m的图象的一个交点的横坐标为2，
（1）求关于x的一元二次方程x²-（m-1）x+m-4=0的解．
（2）若将抛物线C₁：y=x²-（m-1）x+m-4绕原点旋转180°，得到图象C₂，点P为x轴上的一个动点，过点P作x轴的垂线，分别与图象C₁、C₂交于M、N两点，当线段MN的长度最小时，求点P的坐标．

Answer 1

（1）解：∵直线y=（m-1）x+3与函数y=x²+m的图象的一个交点的横坐标为2，
∴2（m-1）+3=4+m
解得m=3
将m=3代入原方程化为x²-2x-1=0，
解得x₁=1+，x₂=1-．

（2）解：将m=3代入得抛物线：y=x²-2x-1=（x-1）²-2，把抛物线绕顶点旋转180°，
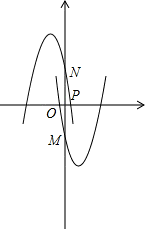
可得新抛物线的解析式的二次项的系数为-1，顶点变为（-1，2），
∴所求的抛物线解析式为：y=-（x+1）²+2=-x²-2x+1，
∴将抛物线y=x²-2x-1绕原点旋转180°得到的图象C₂的解析式为：y=-x²-2x+1．
设P（x，0），则M（x，x²-2x-1），N（x，-x²-2x+1），
∴MN=（x²-2x-1）-（-x²-2x+1）=2x²+2，
∴当x=0时，MN的长度最小，此时点P的坐标为（0，0）．
分析：（1）将两函数联立，求出m即可得到方程，求解即可；
（2）利用二次函数旋转180°后，系数之间的关系，得出新函数的解析式，在表示出M，N的坐标，即可解决．
点评：此题主要考查了一元二次方程的判别式，以及一次函数与二次函数的综合应用，还有二次函数的旋转等，题目综合性较强．