练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．26-（$\frac{7}{9}$-$\frac{11}{12}$+$\frac{1}{6}$）×（-6）2．

    分析 原式先计算乘方运算，再计算乘法运算，最后算加减运算即可得到结果．

    解答 解：原式=26-（$\frac{7}{9}$-$\frac{11}{12}$+$\frac{1}{6}$）×36=26-28+33-6=25．

    点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．菱形ABCD的对角线AC=24，BD=10，则菱形的周长为（　　）
    A．20B．48C．52D．60

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．各边长度都是整数、最大边长为11的三角形共有36个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．化简$\frac{4}{x-4}$+$\frac{x}{4-x}$的结果是（　　）
    A．-1B．1C．-3D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

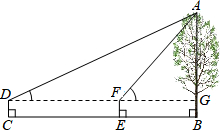    6．如图，小明同学用仪器测量一棵大树AB的高度，在C处测得∠ADG=30°，在E处测得∠AFG=60°，CE=8米，仪器高度CD=1.4米．
    （精确到个位，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{5}$≈2.23）
    （1）求AF的长度；
    （2）求这棵树AB的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

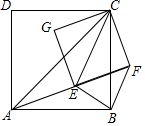    16．如图，四边形ABCD，和四边形CFEG都是正方形，连接AC、AE、BF、CE．
    （1）求证：△CAE∽△CBF；
    （2）若点A、E、F在一条直线上，BC与EF相交于点P，求证：PB•PE=PC•PF；
    （3）当∠CAE+∠CBE=90°，BE=1，AE=2时，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：先化简：（$\frac{{a}^{2}+9}{a}$-6）÷$\frac{{a}^{2}-9}{{a}^{2}+3a}$，再找一个适合的a值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图1，已知E是边长为1的正方形ABCD对角线BD上一动点，点E从B点向D点运动（与B、D不重合），过点E作直线GH平行于BC，交AB于点G，交CD于点H；连接AE，过点E作EF⊥AE于点E，交CD（或CD的延长线）于点F．
    （1）在图1中判断△AEF是什么三角形；
    （2）点E在运动过程中（图1、图2），四边形AFHG的面积是否发生变化？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列说法正确的是（　　）
    A．为了解苏州市中学生的睡眠情况，应该采用普查的方式
    B．某种彩票的中奖机会是1%，则买100张这种彩票一定会中奖
    C．一组数据1，5，3，2，3，4，8的众数和中位数都是3
    D．若甲组数据的方差s甲2=0.1，乙组数据的方差s乙2=0.2，则乙组数据比甲组数据稳定

    查看答案和解析>>

    同步练习册答案