
【题目】如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线 ![]() 上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
【答案】2 ![]()
【解析】解:连接AP,依题可得:要使PQ最小,只要AP最小即可,即AP垂直直线,
设直线与x轴交于C(4,0),与y轴交于B(0,3),
在Rt△COB中,
∵CO=4,BO=3,
∴AB=5,
∴sinA=![]() =
=![]() ,
,
在Rt△CPA中,
∵A(-1,0),
∴AC=5,
∴sinA=![]() =
=![]() =
=![]()
∴PA=3,
在Rt△QPA中,
∵QA=1,PA=3,
∴PQ=![]() =
=![]() =2
=2![]()
【考点精析】解答此题的关键在于理解点到直线的距离的相关知识,掌握从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】某服装商预测一种应季衬衫能畅销市场,就用8000元购进一批衬衫,面市后果然供不应求,服装商又用17600元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了8元.商家销售这种衬衫时每件定价都是100元,最后剩下10件按8折销售,很快售完.在这两笔生意中,商家共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.

证明:∵∠AGB=∠EHF
∠AGB=___________(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC(____________________________________)
∴∠_________=∠DBA(________________________________)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥_______(__________________________________)
∴∠A=∠F(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点A B. 点B
C. A,B之间 D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9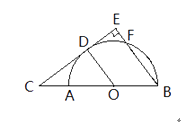
(1)求证:△COD∽△CBE;
(2)求半圆O的半径 ![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
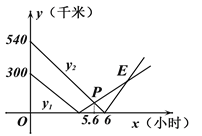
【题目】高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲乙两车离B的距离![]() 、
、![]() (千米)与行驶时间x(小时)之间的函数关系图象如图所示,交点P的横坐标为5.6,观察图象,给出下列结论:
(千米)与行驶时间x(小时)之间的函数关系图象如图所示,交点P的横坐标为5.6,观察图象,给出下列结论:
①A、C之间的路程为840千米;②乙车比甲车每小时快30千米;③当乙车到A点时,甲车距离B点250千米;④点E的坐标为(8,180).其中正确的有________________(填正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
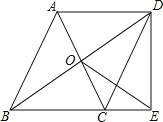
【题目】已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.
(1)求证:DE⊥BE;
(2)设CD与OE交于点F,若OF2+FD2=OE2,CE=3,DE=4,求线段CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com