
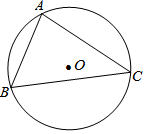
 如图,△ABC内接于⊙O,若⊙O的半径为6,∠B=60°,求AC的长.
如图,△ABC内接于⊙O,若⊙O的半径为6,∠B=60°,求AC的长.  提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,圆中的弦AB与弦CD垂直于点E,点F在$\widehat{BC}$上,$\widehat{AC}$=$\widehat{BF}$,直线MN过点D,且∠MDC=∠DFC,求证:直线MN是该圆的切线.
如图,圆中的弦AB与弦CD垂直于点E,点F在$\widehat{BC}$上,$\widehat{AC}$=$\widehat{BF}$,直线MN过点D,且∠MDC=∠DFC,求证:直线MN是该圆的切线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
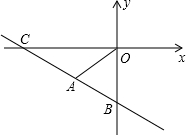 如图,一次函数y=ax-b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于B(0,-4),且OA=AB,△AOB的面积为6.
如图,一次函数y=ax-b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于B(0,-4),且OA=AB,△AOB的面积为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰三角形ABC中,AB=AC=5cm,BC=6cm,动点P从点A出发,沿路线A-B-C匀速运动,速度为1cm/s,运动到C点停止,设运动时间为t(s),△APC的面积为y(cm2).
如图,等腰三角形ABC中,AB=AC=5cm,BC=6cm,动点P从点A出发,沿路线A-B-C匀速运动,速度为1cm/s,运动到C点停止,设运动时间为t(s),△APC的面积为y(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,一根木棒AB长为2,斜靠在与地面OM垂直的墙壁ON上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿NO向下滑动到A′,B端沿直线OM向右滑动到B′,若AA′=$\sqrt{3}$-1,则木棒的中点从P随之运动到P′所经过的路径长为$\frac{π}{6}$.
如图所示,一根木棒AB长为2,斜靠在与地面OM垂直的墙壁ON上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿NO向下滑动到A′,B端沿直线OM向右滑动到B′,若AA′=$\sqrt{3}$-1,则木棒的中点从P随之运动到P′所经过的路径长为$\frac{π}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com