
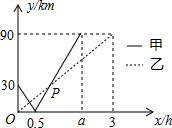
 在一条笔直的河道上依次有A,B,C,三个港口在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.
在一条笔直的河道上依次有A,B,C,三个港口在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图. =60(km/h),
=60(km/h),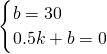 ,
,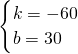
 ,
,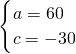
 ;
;

科目:初中数学 来源: 题型:
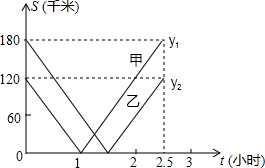 一条笔直的公路上依次有B、A、C三地,BC两地相距300千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(千米)与行驶时间t(时)的关系如图所示,则甲、乙两车相遇时离A地的距离为
一条笔直的公路上依次有B、A、C三地,BC两地相距300千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(千米)与行驶时间t(时)的关系如图所示,则甲、乙两车相遇时离A地的距离为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏泰兴实验初级中学八年级上期末考试数学试卷(带解析) 题型:解答题
在一条笔直的河道上依次有A、B、C三个港口,甲、乙两船同时分别从A、B 港口出发,沿直线匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示(点P、Q为图象的交点).
(1)填空:A、C两港口间的距离为 km,a= ;
(2)求y1与x的函数关系式,并写出自变量x的取值范围;
(3)求图中点P的坐标,并解释该点坐标所表示的实际意义。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏泰兴实验初级中学八年级上期末考试数学试卷(解析版) 题型:解答题
在一条笔直的河道上依次有A、B、C三个港口,甲、乙两船同时分别从A、B 港口出发,沿直线匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示(点P、Q为图象的交点).
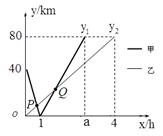
(1)填空:A、C两港口间的距离为 km,a= ;
(2)求y1与x的函数关系式,并写出自变量x的取值范围;
(3)求图中点P的坐标,并解释该点坐标所表示的实际意义。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com