
【题目】如图,在 ![]() 中,
中, ![]() ,AB=BC,A,B的坐标分别为
,AB=BC,A,B的坐标分别为 ![]() ,将
,将 ![]() 绕点P旋转
绕点P旋转 ![]() 后得到
后得到 ![]() ,其中点B的对应点
,其中点B的对应点 ![]() 的坐标为
的坐标为 ![]() .
.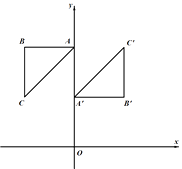
(1)求出点C的坐标;
(2)求点P的坐标,并求出点C的对应点 ![]() 的坐标.
的坐标.
【答案】
(1)解:∵A、B 的坐标分别为(0,4)(-2,4) ,
∴AB=2,
∴BC=AB=2,
∵∠B=90°,AB∥x轴,
∴BC⊥x轴,
所以点C的坐标为(-2,2)
(2)解:∵B点的对应点为B’点,
∴点P为BB’的中点,
∴点P的横坐标为: ![]() =0,纵坐标为:
=0,纵坐标为: ![]() =3,
=3,
即P(0,3);
设C’(x,y),
根据旋转的性质可知:点P为CC’的中点,
∴ ![]() =0,
=0, ![]() =3,
=3,
解得:x=2,y=4,
∴C’(2,4).
【解析】直接利用平移的性质得出平移规律即可;利用旋转的性质得出对应点位置进而得出答案,
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足|x1|+|x2|=|x1x2|-1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸板ABC放置在锐角△PMN上,使该直角三角形纸板的两条直角边AB,AC分别经过点M,N.
(发现)
(1)如图1,若点A在△PMN内,当∠P=30°时,则∠PMN+∠PNM=______°,∠AMN+∠ANM=______°,∠PMA+∠PNA=______°.
(2)如图2,若点A在△PMN内,当∠P=50°时,∠PMA+∠PNA=______°.
(探究)
(3)若点A在△PMN内,请你判断∠PMA,∠PNA和∠P之间满足怎样的数量关系,并写出理由.
(应用)
(4)如图3,点A在△PMN内,过点P作直线EF∥AB,若∠PNA=16°,则∠NPE=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile,它们离开港口一个半小时后相距30nmile,且知道“远航”号沿东北方向航行,那么“海天”号航行的方向是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某小区要用篱笆围成一矩形花坛,花坛的一边用足够长的墙,另外三边所用的篱笆之和恰好为 ![]() 米.
米.
(1)求矩形 ![]() 的面积(用
的面积(用 ![]() 表示,单位:平方米)与边
表示,单位:平方米)与边 ![]() (用
(用 ![]() 表示,单位:米)之间的函数关系式(不要求写出自变量
表示,单位:米)之间的函数关系式(不要求写出自变量 ![]() 的取值范围);怎样围,可使花坛面积最大?
的取值范围);怎样围,可使花坛面积最大?
(2)如何围,可使此矩形花坛面积是 ![]() 平方米?
平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( ) 
A.55°
B.70°
C.125°
D.145°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com