
【题目】我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.如图,在△ABC中,AB>AC,点D,E分别在AB,AC上,设CD,BE相交于点O,如果∠A是锐角,∠DCB=∠EBC=![]() ∠A.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
∠A.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
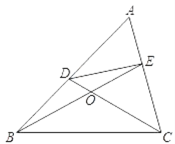
【答案】存在等对边四边形,是四边形DBCE,见解析
【解析】
作CG⊥BE于G点,作BF⊥CD交CD延长线于F点,证明△BCF≌△CBG,得到BF=CG,再证∠BDF=∠BEC,得到△BDF≌△CEG,故而BD=CE,即四边形DBCE是等对边四边形.
解:此时存在等对边四边形,是四边形DBCE.
如图,作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.
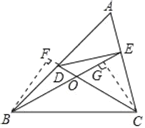
∵∠DCB=∠EBC=![]() ∠A,BC为公共边,
∠A,BC为公共边,
∴△BCF≌△CBG,
∴BF=CG,
∵∠BDF=∠ABE+∠EBC+∠DCB,∠BEC=∠ABE+∠A,
∴∠BDF=∠BEC,
∴△BDF≌△CEG,
∴BD=CE
∴四边形DBCE是等对边四边形.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=![]() (x>0)和y=
(x>0)和y=![]() (x<0)的图象分别交于点P,Q.
(x<0)的图象分别交于点P,Q.
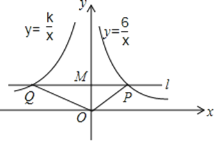
(1)求P点的坐标;
(2)若△POQ的面积为9,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在地面上竖直安装着AB、CD、EF三根立柱,在同一时刻同一光源下立柱AB、CD形成的影子为BG与DH.

(1)填空:判断此光源下形成的投影是: 投影.
(2)作出立柱EF在此光源下所形成的影子.
查看答案和解析>>
科目:初中数学 来源: 题型:
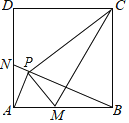
【题目】如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为⊙O上一点,点C在直径AB的延长线上,且∠CDB=∠CAD,过点A作⊙O的切线,交CD的延长线于点E.

(1)判定直线CD与⊙O的位置关系,并说明你的理由;
(2)若CB=4,CD=8,①求圆的半径.②求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A>∠B,分别以点A,C为圆心,大于![]() AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于
AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于![]() BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
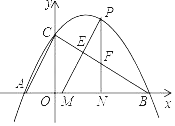
【题目】如图,二次函数y=ax2+bx+![]() 的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
(1)求这个二次函数的解析式;
(2)求线段PE最大值,并求出线段PE最大时点P的坐标;
(3)若S△PMN=3S△PEF时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
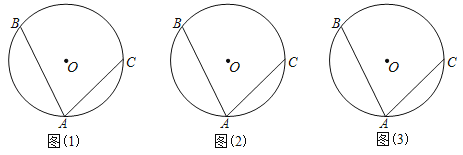
【题目】作图题:⊙O上有三个点A,B,C,∠BAC=70°,请画出要求的角,并标注.
(1)画一个140°的圆心角;(2)画一个110°的圆周角;(3)画一个20°的圆周角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com