
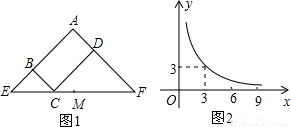
 ;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3
;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3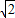 ,CF=3
,CF=3 ,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EC=
,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EC= ,而EM=3
,而EM=3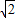 ;由于EC•CF=
;由于EC•CF= x(6
x(6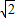 -
- x)配方得到-2(x-3)2+18,根据二次函数的性质得当0<x<3时,EC•CF的值随x的增大而增大;利用等腰直角三角形的性质BE•DF=BC•CD=xy,然后再根据反比例函数的性质得BE•DF=9,其值为定值.
x)配方得到-2(x-3)2+18,根据二次函数的性质得当0<x<3时,EC•CF的值随x的增大而增大;利用等腰直角三角形的性质BE•DF=BC•CD=xy,然后再根据反比例函数的性质得BE•DF=9,其值为定值.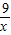 ;
; BC=3
BC=3 ,CF=
,CF= CD=3
CD=3 ,C点与M点重合,则EC=EM,所以A选项错误;
,C点与M点重合,则EC=EM,所以A选项错误; ,而EM=3
,而EM=3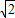 ,所以B选项错误;
,所以B选项错误; x(6
x(6 -
- x)=-2(x-3)2+18,所以当0<x<3时,EC•CF的值随x的增大而增大,所以C选项错误;
x)=-2(x-3)2+18,所以当0<x<3时,EC•CF的值随x的增大而增大,所以C选项错误;

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
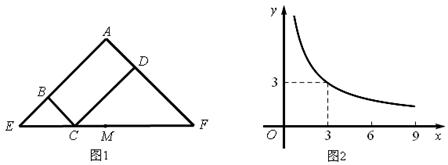
 (2013•安徽)图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
(2013•安徽)图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽蚌埠六中九年级11月阶段检测数学试卷(解析版) 题型:选择题
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )

A.当x=3时,EC<EM B.当y=9时,EC>EM
C.当x增大时,EC•CF的值增大 D.当y增大时,BE•DF的值不变
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(安徽卷)数学(解析版) 题型:选择题
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是
A.当x=3时,EC<EM B.当y=9时,EC>EM
C.当x增大时,EC·CF的值增大。 D.当y增大时,BE·DF的值不变。
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(安徽卷)数学(带解析) 题型:单选题
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是
| A.当x=3时,EC<EM | B.当y=9时,EC>EM |
| C.当x增大时,EC·CF的值增大。 | D.当y增大时,BE·DF的值不变。 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com