分析:要证明AE⊥BE,只要证明∠AEB是直角即可,当∠AEB=90°时,∠AEC+∠DEB=90°.又因为∠DBE+∠DEB=90°,那么要证明AE⊥EB,只要证明∠AEC=∠DBE即可.那么我们可通过构建全等三角形来实现.过E作EF∥BC交BD于F,∠DEF=∠DCB=45°.根据E是CD中点,那么EF是直角三角形BCD的中位线,那么EF=
BC=AC,CE=BF,直角三角形EFB和ACE中,已知的条件有EF=AC,CE=BF,只要再得出两边的夹角相等即可,我们发现∠ACE=∠BFE=90°+45°=135°,由此就凑齐了三角形全等的条件,两三角形就全等了.∠AEC=∠DBE.
解答:证明:过E作EF∥BC交BD于F.
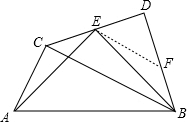
∵∠ACE=∠ACB+∠BCE=135°,∠DFE=∠DBC=45°,
∴∠EFB=135°.
又EF=
BC,EF∥BC,AC=
BC,
∴EF=AC,CE=FB.
∴△EFB≌△ACE.
∴∠CEA=∠DBE.
又∵∠DBE+∠DEB=90°,
∴∠DEB+∠CEA=90°.
故∠AEB=90°.
∴AE⊥EB.
点评:本题考查了直角三角形的性质,全等三角形的判定等知识点,利用全等三角形得出线段和角相等是解此类题的关键.

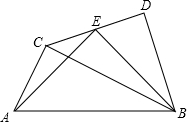 在△ABC中,∠ACB=90°,AC=
在△ABC中,∠ACB=90°,AC=


 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=