
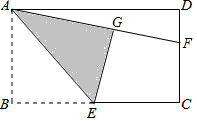
 如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )
如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{6}$ | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{3}$ |
分析 首先连接EF,由折叠的性质可得BE=EG,又由E是BC边的中点,可得EG=EC,然后证得Rt△EFG≌Rt△EFC(HL),继而求得线段AF的长,再利用勾股定理求解,即可求得答案.
解答 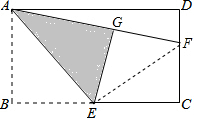 解:连接EF,
解:连接EF,
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EG,
∴EG=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EGF=∠B=90°,
∵在Rt△EFG和Rt△EFC中,
$\left\{\begin{array}{l}{EG=EC}\\{EF=EF}\end{array}\right.$,
∴Rt△EFG≌Rt△EFC(HL),
∴FG=CF=2,
∵在矩形ABCD中,AB=CD=CF+DF=2+1=3,
∴AG=AB=3,
∴AF=AG+FG=3+2=5,
∴BC=AD=$\sqrt{A{F}^{2}-D{F}^{2}}$=$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$.
故选B.
点评 此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.注意证得FG=FC是关键.


科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$×4$\sqrt{2}$=12$\sqrt{2}$ | B. | $\sqrt{(-3)^{2}}$=-3 | C. | ($\sqrt{8}$-$\sqrt{3}$)×$\sqrt{6}$=4$\sqrt{3}$-9$\sqrt{2}$ | D. | (4$\sqrt{2}$-3$\sqrt{6}$)÷2$\sqrt{2}$=2-$\frac{3}{2}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.
如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
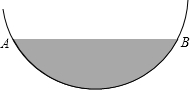 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
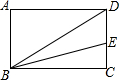 如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )| A. | $\frac{4}{3}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
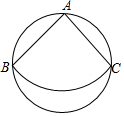 如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 3$\sqrt{2}$cm | B. | 2$\sqrt{3}$cm | C. | 6cm | D. | 12cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com