
分析 把①化为x=±2y,把②化为x+y=±2,重新组成方程组,解二元一次方程组即可.
解答 解:$\left\{\begin{array}{l}{{x}^{2}-4{y}^{2}=0①}\\{{x}^{2}+2xy+{y}^{2}=4②}\end{array}\right.$,
由①得,x=±2y,
由②得,x+y=±2,
则$\left\{\begin{array}{l}{x=2y}\\{x+y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=-2y}\\{x+y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=-2y}\\{x+y=-2}\end{array}\right.$$\left\{\begin{array}{l}{x=2y}\\{x+y=-2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=\frac{4}{3}}\\{{y}_{1}=\frac{2}{3}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=-2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{3}=-4}\\{{y}_{3}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{4}=-\frac{4}{3}}\\{{y}_{4}=-\frac{2}{3}}\end{array}\right.$.
点评 本题考查的是二元二次方程组的解法,把二元二次方程根据平方差公式和完全平方公式进行变形化为两个二元一次方程是解题的关键.


科目:初中数学 来源: 题型:解答题
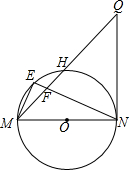 如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为$\widehat{MH}$上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN.
如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为$\widehat{MH}$上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的平面直角坐标系中,每个小正方形的边长均为1,△ABC的顶点都在格点上.
在如图所示的平面直角坐标系中,每个小正方形的边长均为1,△ABC的顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
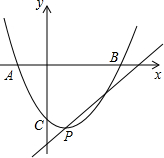 已知抛物线y=ax2-2ax+c与x轴交于A、B两点,与y轴交于点C.其中.A(-1,0),C(0,-3).
已知抛物线y=ax2-2ax+c与x轴交于A、B两点,与y轴交于点C.其中.A(-1,0),C(0,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com